El procedimiento de la fuerza ficticia: un símil del método del potencial unidimensional equivalente en la solución del problema de Kepler

The Fictitious Force Procedure: A Simile of the Equivalent One-Dimensional Potential Method in Solving the Kepler Problem

Autores:
  • Hernando González Sierra
  • Cristian Camilo Toledo Chavarro
DOI 10.22430/22565337.1612 Figuras

Recibido: 05 de Marzo de 2020
Aceptado: 24 de junio de 2020

 

Resumen

Se elabora un procedimiento alternativo al del método del potencial unidimensional equivalente para describir las características cualitativas del movimiento de dos partículas bajo el efecto de fuerzas centrales, aplicándolo al caso específico del problema de Kepler relacionado con el movimiento de los planetas alrededor del sol; es decir, para la ley de fuerza atractiva inversamente proporcional al cuadrado de la distancia. El nuevo tratamiento denominado “Método de la fuerza ficticia” es implementado en el contexto de la Mecánica Clásica y difiere del método del potencial unidimensional equivalente a que en lugar de emplear el potencial ficticio se usa la fuerza ficticia; desde esta última perspectiva, se identifica que se está tratando con un símil, ya que se actúa en la misma área del conocimiento, y que se refiere a una nueva herramienta de características geométricas para obtener soluciones de tipo cualitativo a los efectos cinemáticos cuando se tienen fuerzas centrales entre dos cuerpos. El símil, para el caso particular tratado en el presente, conduce a los mismos resultados del método del potencial unidimensional equivalente, que proporciona secciones cónicas como trayectorias para la fuerza atractiva del cuadrado inverso entre los cuerpos, pero tiene la ventaja de que se pueden cuantificar los valores de la fuerza efectiva para algunas órbitas específicas. Al igual que el método del potencial unidimensional equivalente, el símil de la fuerza ficticia puede ser aplicado a otras leyes de fuerzas centrales de forma arbitraria y, lo más importante, el procedimiento podría mostrar su potencialidad en otras áreas de la física contemporánea, ciencias físicas y afines e ingenierías.

Palabras clave: fuerzas centrales, masa reducida, fuerza ficticia, energía potencial.

Abstract

An alternative procedure to the equivalent one-dimensional potential method is developed to describe the qualitative characteristics of the motion of two particles under the effect of central forces, applying it to the specific case of the Kepler problem related to the otion of the planets around the sun that is, for the inversely proportional attractive force law, the square of the distance. The new treatment called ¨Fictitious Force Method¨ is implemented in the context of Classical Mechanics and differs from the equivalent one-dimensional potential method in that instead to use the fictitious potential, the fictitious force is used; from this last perspective, it is identified that one is dealing with a simile, since it is acting within the same area of knowledge, and that it refers to a new tool with geometric characteristics to obtain qualitative solutions to the cinematic effects when you have central forces between two bodies. The simile, for the particular case treated, leads to the same results of the equivalent one-dimensional potential method that provides conic sections as trajectories for the attractive force of the inverse square between the bodies, but has the advantage that the values ​​of the force can be quantified effective for some specific orbits. Like the equivalent one-dimensional potential method, the fictive force simile can be arbitrarily applied to other central force laws and, most importantly, the procedure could show its potential in other areas of Contemporary Physics, Physical Sciences and ties to Engineering.

Keywords: Central forces, reduced mass, fictitious force, potential energy.

1. INTRODUCCIÓN

El método del potencial unidimensional equivalente es una herramienta de análisis que permite estudiar las características cualitativas del movimiento de dos cuerpos bajo la acción de fuerzas centrales [1].

La descripción del movimiento de los planetas alrededor del sol es conocido como el problema de Kepler [2]; no obstante, las características dinámicas de la solución se pueden extender a cuerpos sometidos a cualquier fuerza central en el dominio de la Mecánica Clásica [3].

El movimiento de dos cuerpos bajo el efecto de una fuerza central se simplifica por su reducción al problema equivalente de un solo cuerpo [4]. La reducción se logra describiendo el movimiento de un solo cuerpo, al cual se le asocia una masa reducida `μ`, que se encuentra sometida a una fuerza central. Esta primera adaptación, que involucra el concepto de centro de masa, posibilita el uso el método del potencial unidimensional equivalente.

La descripción cualitativa del movimiento hace referencia a las posibles trayectorias que sigue la partícula de masa reducida `μ` y que se presentan como secciones cónicas [5].

Para obtener una solución al problema de Kepler es necesario estudiar la dinámica a partir del tratamiento de las ecuaciones de movimiento para la ley de cuadrado inverso, usando la ecuación diferencial de la órbita o su forma integral [6]. Las formulaciones de Newton, Lagrange y Hamilton pueden ser usadas indistintamente para obtener la dinámica del problema de fuerzas centrales entre dos cuerpos [7].

En este artículo se presenta un símil del método del potencial unidimensional equivalente, el cual se ha denominado “Método de la fuerza ficticia”. El concepto de símil es diferente al de analogía y está caracterizado porque las correspondencias de comparación entre los distintos elementos se ubican dentro del mismo campo del conocimiento [8], mientras que en las analogías los elementos se introducen en dos áreas diversas [9]. En la elaboración de la estructura de la Teoría Electromagnética, J. C. Maxwell utilizó analogías extraídas de la hidrodinámica.

La connotación símil estructural se refiere a que dos principios, aparentemente distintos, dan cuenta de un mismo efecto; un caso particular es el de la ley de Snell [10]. Algunos autores hacen uso de los conceptos de analogías y símiles en sus trabajos de investigación [11]; en este sentido esos conceptos contribuyen al pensamiento científico y son efectivos en la elaboración de modelos y teorías.

Esta contribución está distribuida de la siguiente manera: en la segunda sección se hace alusión al movimiento de dos cuerpos bajo la acción de fuerzas centrales, en la tercera sección se halla la reducción del problema de dos cuerpos a la equivalente de un solo cuerpo, en la cuarta sección se explica brevemente el método unidimensional equivalente en el tratamiento del problema de fuerzas centrales entre dos cuerpos, y en la quinta sección, que es la parte central de la contribución, se plantea el desarrollo del símil del problema unidimensional equivalente. Finalmente, en la sexta sección se expone un análisis del símil, y se elaboran contrastaciones con el método del potencial unidimensional equivalente, a fin de mostrar las diferencias, las similitudes, las ventajas y desventajas.

El método de la fuerza ficticia puede extenderse al tratamiento de problemas que se ubican en diversos campos de las ciencias e ingenierías, como en el caso del movimiento de los cuerpos celestes como planetas, satélites, estrellas [12], agujeros negros binarios [13], estrellas de neutrones [14], colisiones a altas energías en física atómica y molecular [15], modelamiento para análisis químico [16], potenciales en moléculas diatómicas [17], materia condensada o física del estado sólido [18], perspectivas de física contemporánea [19].

2. EL PROBLEMA DE FUERZAS CENTRALES ENTRE DOS CUERPOS

El movimiento de un sistema físico conformado por dos cuerpos que interactúan por medio de una fuerza dirigida en la dirección de la recta que une los dos centros, fuerza central, es uno de los problemas más importantes de la Física.

Antes de formularse la Mecánica Cuántica, la imagen clásica del átomo de hidrógeno se representaba por el efecto de la fuerza de atracción entre el electrón y el protón, una fuerza de tipo central dada por la ley de Coulomb [20].

El problema de Kepler se refiere a la solución completa del movimiento de un planeta bajo el efecto de la fuerza gravitacional ejercida por el sol, que es una fuerza central que varía con el inverso del cuadrado de la distancia [21].

3. REDUCCIÓN AL PROBLEMA EQUIVALENTE DE UN SOLO CUERPO

Dos cuerpos de masas `m_1` y `m_2` que interactúan bajo el efecto de una fuerza central (Fig. 1) pueden ser representados por un solo cuerpo de masa reducida `μ` dada por [22] en (1):

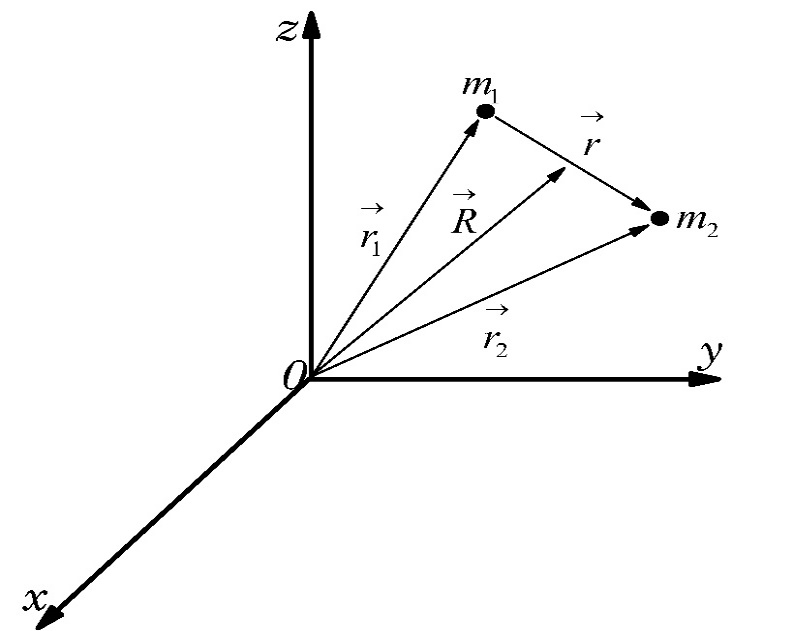
Fig. 1. Movimiento de dos partículas bajo el efecto de una fuerza central. Fuente: [22].

La simplificación radica en que ahora se tiene solamente una partícula de masa reducida μ ubicada a una distancia |`r`→| de un centro de fuerzas. El vector `r`→ está dado como en (2):

El centro de masa del sistema de dos partículas se define mediante (3):

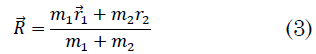
La función Lagrangiana de la partícula de masa reducida `μ` es [23] en (4):

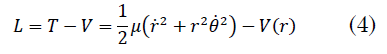
T es la energía cinética y `V(r)` la energía potencial. La función Lagrangiana de la partícula de masa reducida `μ`, ecuación (4), tiene dos grados de libertad, las dos coordenadas polares `r` y 𝜃.

Dado que la coordenada 𝜃 es cíclica, la cantidad de movimiento angular es una constante del movimiento y su magnitud expresada mediante (5):

La conservación del momento angular es una propiedad inherente a toda fuerza central, el movimiento de la partícula de masa reducida `μ` tiene lugar en un plano, lo cual facilita el empleo de coordenadas polares, como coordenadas generalizadas, en (4). La energía potencial solo depende de `r`, siendo esféricamente simétrica.

La función Lagrangiana expresada en términos del momento angular contiene tres términos [23] como en (6):

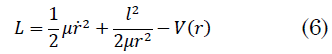
La conservación del momento angular hace que la función Lagrangiana solo tenga una coordenada independiente, grado de libertad, que es la coordenada radial `r`.

Para esta Lagrangiana la ecuación del movimiento radial es (7):

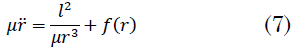
En donde `f(r)` es la fuerza central que actúa sobre la partícula, que deriva de un potencial `V(r)`, tal que `f(r)` = `-``(dV(r))/dr`

La energía total de la partícula es una constante del movimiento como en (8):

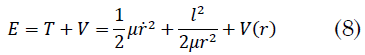
El sistema de dos partículas de masas `m_1` y `m_2` necesita 6 coordenadas para especificar su configuración; la reducción al sistema equivalente de un solo cuerpo disminuye el número de grados de libertad a 3; la naturaleza de fuerza central elimina otro grado de libertad y, finalmente, la conservación del momento angular deja una única coordenada independiente para especificar la configuración del sistema de dos partículas.

4. EL MÉTODO DEL POTENCIAL UNIDIMENSIONAL EQUIVALENTE

El término `l^2/(2μr^(2))` en (8) puede ser interpretado como una energía potencial, que puede sumarse a `V(r)` para dar un potencial ficticio (9):

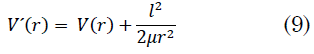
Sustituyendo (9) en (8) nos queda (10)

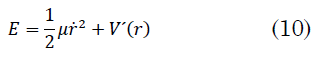
Interpretado `l^2/(2μr^(2))` como una energía potencial, se le puede asociar una fuerza `fc` tal que (11):

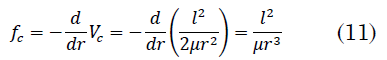
A `fc` antiguamente se le llamó fuerza centrífuga; este nombre ha sido abolido de la literatura científica porque causa confusión y no es adecuado [24]. Acá simplemente se expresa que `fc` deriva del potencial `l^2/(2μr^(2))`, y que el potencial ficticio `V´(r)`, en (9), es la suma del potencial real `V´(r)` y `l^2/(2μr^(2))`.

Relacionado con el potencial ficticio está la fuerza ficticia `f’(r)`, estando conectados por `f’(r)` =- `(dV'(r))/(dr)` En (12):

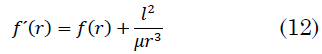
El método del potencial unidimensional equivalente consiste en obtener una solución cualitativa, para el potencial ficticio (8), dado un potencial real `V(r)`.

Esta solución es plausible adicionando la ecuación de la energía (8).

Para el problema de Kepler la fuerza real y el potencial real están dados, respectivamente, por (13) y (14):

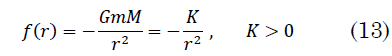
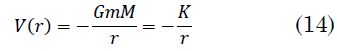
El potencial ficticio es (15):

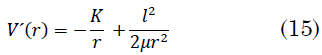
La energía total se expresa en términos del potencial ficticio mediante (16):

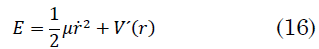
De acuerdo con los valores de la energía se pueden clasificar las diversas trayectorias; algunas veces es conveniente hacerlo a través de un parámetro que caracteriza las secciones cónicas que es la excentricidad ε. De esta forma se verifica que [25]:

-Hipérbola  `E> 0   ε> 1`

-Parábola  `E= 0   ε= 1`

-Elipse  `E< 0   ε< 1`

- Círculo  `E< 0   ε= 0`

La solución gráfica de (15), proporciona las características cualitativas del movimiento (Fig. 2) para los diversos valores de la energía da los siguientes resultados:

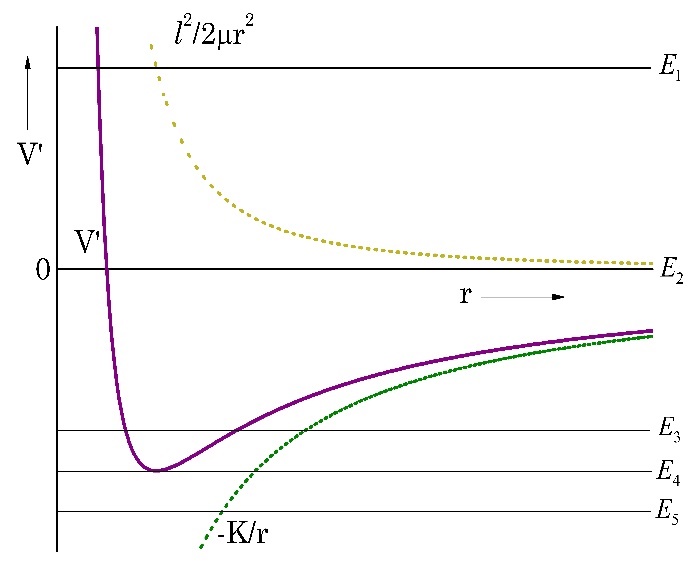
Fig. 2. Método del potencial unidimensional equivalente. Fuente: [22].

    a) `E_1> 0`. La partícula se aproxima al centro de fuerzas una distancia mínima `r_1`, lugar en el que invierte su movimiento dirigiéndose a la región de valores `r> r_1`. La trayectoria de la partícula es no acotada (órbita hiperbólica).

    b) `E_2= 0`. La partícula se acerca al centro de fuerzas una distancia mínima `r_2`. Al igual que el caso a) se tiene una trayectoria no acotada (órbita parabólica).

    c) `E_3< 0`. `E_3` intercepta a `V´(r)` en dos puntos denominados puntos de retroceso o distancias absidales. La trayectoria de la partícula es acotada (órbita elíptica).

    d) `E_4< 0`. Ubicada en el mínimo de `V´(r)`, existe un único punto de retroceso `r_0` que corresponde al radio de una órbita circular.

    e) `E_5< V´_(min)`. Orbita no permitida.

Los puntos de retroceso o distancias absidales son las distancias al centro de fuerzas para las cuales `r ˙ =0` Para estos puntos de retroceso se verifica que (17):

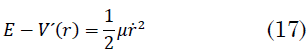
El método del potencial unidimensional equivalente da solución al problema de Kepler como una de las secciones cónicas, dependiendo cada una de ellas del valor de la energía de la partícula.

5. EL MÉTODO DE LA FUERZA EFECTIVA

Este método consiste en resolver gráficamente la ecuación de la fuerza efectiva dada por (12). Para el problema de Kepler la fuerza real sigue la ley de cuadrado inverso de la distancia (18)

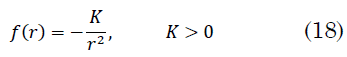
La ecuación a solucionar gráficamente es (19):

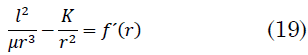
Junto con la ecuación de la energía la cual permite determinar los puntos de retroceso (20)

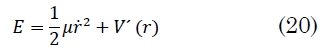
La ecuación de la energía es usada en el procedimiento de la fuerza ficticia; los puntos de retroceso se determinan por la cancelación de `r ˙` en esta última expresión.

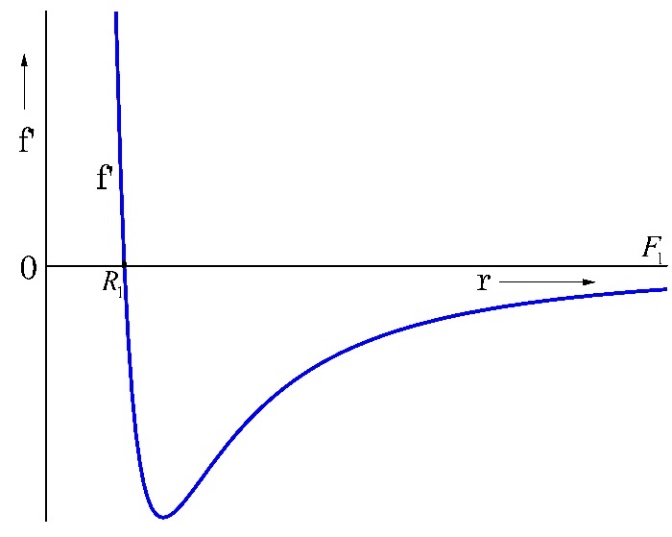
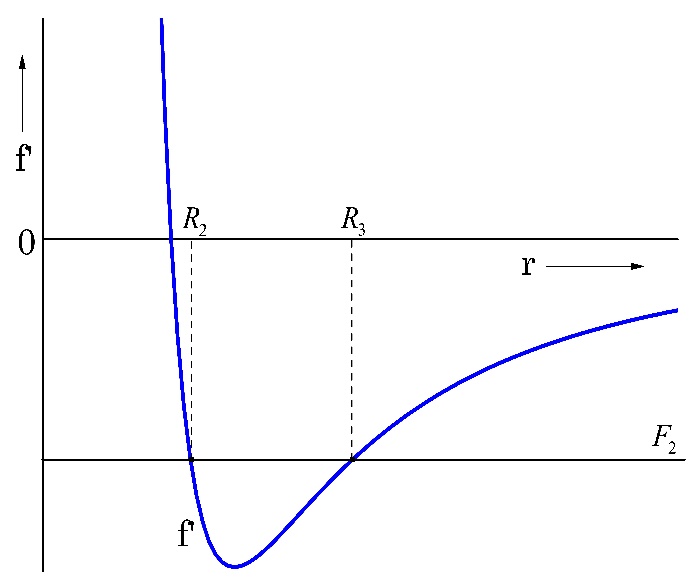
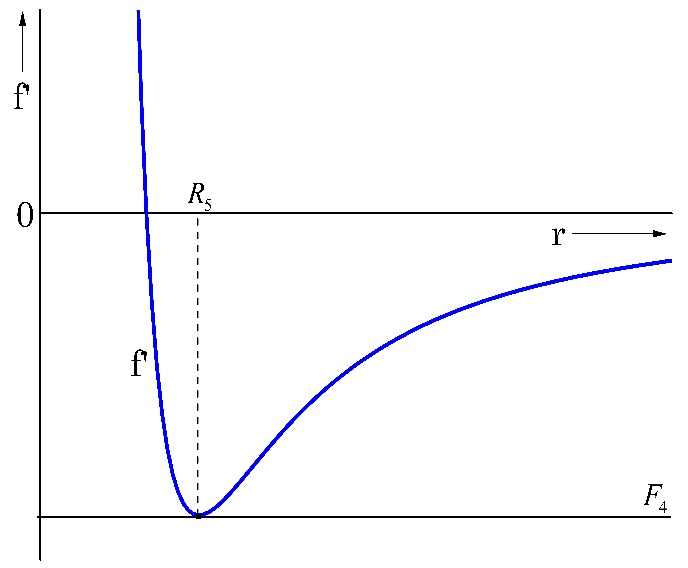
El método de la fuerza ficticia, para el problema de Kepler, es una solución gráfica de (19) para valores arbitrarios de `f´(r)`. La representación gráfica de `f´(r)` se ilustra en la Fig. 3. `F_1, F_2, F_3` y `F_4` son valores arbitrarios de `f´(r)` y que generan los puntos de corte `R_1, R_2, R_3, R_4` y `R_5`, con su intercepción, que se muestran en las gráficas subsecuentes.

En la Fig. 3. se muestran la fuerza real (línea continua inferior) la fuerza `(l^2)/(μr^3)` línea discontinua superior) y la fuerza ficticia (línea sólida).

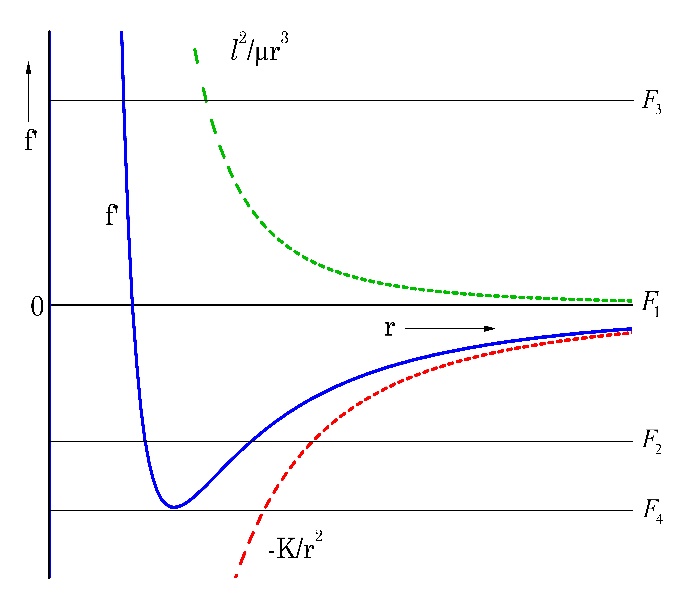
Fig. 3. Método de la fuerza ficticia para la ley de fuerza atractiva del cuadrado inverso. Fuente: elaboración propia.

Para valores pequeños de r la fuerza `(l^2)/(μr^3)` domina a la fuerza real, así que cuando `r`→0 `f´(r)`→`∞`. Para valores grandes de `r`, la fuerza real domina a la fuerza `(l^2)/(μr^3)` o sea, para `r`→ `∞ f´(r)`→`0`.

De acuerdo con la Fig. 3, se tienen las siguientes posibilidades para `f´(r)`:

    a) `f´(r) = F1 = 0`. (Fig. 4)

Fig. 4. Se ilustra la situación `f´(r)=F1=0` Fuente: elaboración propia.

Corresponde a la anulación de la fuerza ficticia; la fuerza real se anula con la fuerza `(l^2)/(μr^3)` quedando (21):

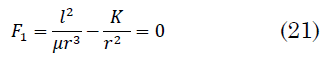
La fuerza ficticia puede ser nula, no así la fuerza real que está definida para un conjunto de valores de `r`, excepto para `r= 0`. `F_1` da un único punto de corte con la condición (22):

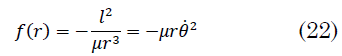
La ecuación (22) es la condición para una órbita circular, es decir, la fuerza real equilibra a la fuerza `- (l^2)/(μr^3)` La órbita contiene solamente la distancia radial, `r ˙` = constante ya que `r ¨ =0` en la ecuación de movimiento radial (7). Existe solo un punto de corte `R_1= R_0` que corresponde a una trayectoria circular.

La ecuación (21) da la restricción (23):

Usando (23) en (17) nos queda (24):

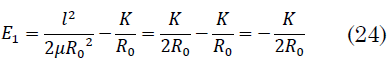
La restricción (23) ocasiona que el punto de corte coincida con el punto de retroceso.

Por lo tanto, `E_1< 0`, así la trayectoria de la partícula es acotada o limitada, el corte `F_1= 0` corresponde a una órbita circular. Como `E_1` y `K` son constantes `R_0` en (24) es constante, por lo que se infiere que la trayectoria corresponde a una órbita circular.

    b) `f´(r)=F_2< 0` (Fig. 5)

Fig. 5. `f´(r)=F_2 < 0`. Se tienen dos puntos de corte que corresponden al intercepto `F_2` con `f´(r)`. Los puntos de corte son `R_2` y `R_3`. Fuente: elaboración propia.

Ahora `(l^2)/(μr^3)` `-` `K/r^2 < 0` que da la restricción (25):

`l^2< μKr` (25)

Usando la restricción dada por (25) en (17), con `E=E_2`, obtenemos (26):

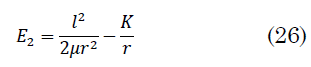
La ecuación (26) es una ecuación de segundo orden en la variable `r`, se tiene dos puntos de retroceso para los cuales `r ˙ = 0` para este caso `F_2 < 0`. La fuerza ficticia, que toma el valor `F_2`, no se anula como en el caso anterior.

De la ecuación (26) y de la condición (25) resulta `E = E_2 < 0`, que se satisface para los puntos de retroceso en donde `r ˙` se anula. Con dos puntos de corte (Fig. 5), `R_2` y `R_3`, situación que corresponde a `E = E_2 < 0` de acuerdo con (26), trayectoria acotada, que corresponde a órbita elíptica para la partícula de masa reducida `μ`.

La ecuación (26) es resuelta para los dos puntos de retroceso `r_2` y `r_3` dados por (27) y (28)

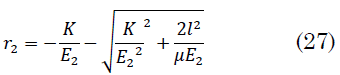
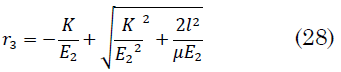
Con estos dos puntos de retroceso que provienen de la ecuación de la energía se determina el semieje mayor de la elipse [26] dado por (29).

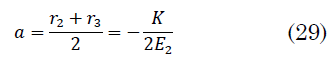
La ecuación (26) se verifica solo para la región `r_2 ≤ r ≤ r_3`, debido a que fuera de esta región la velocidad de la partícula es una cantidad imaginaria, porque se debe satisfacer la ecuación (10).

La energía está relacionada con el semieje mayor de la elipse (30):

Las ecuaciones (24) y (30) son de importancia primordial en el modelo de Bohr del átomo de hidrogeno [27].

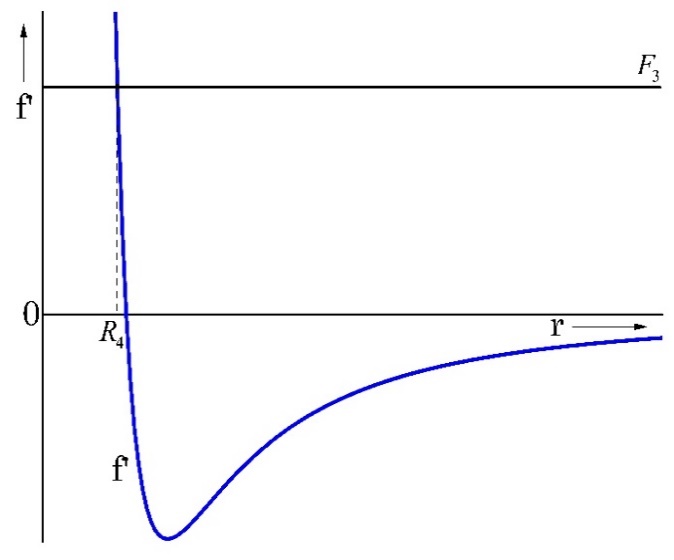
    c) `f´(r) = F_3 > 0`. (Fig. 6)

Fig. 6. `f´(r)=F_3>0`. Valor positivo de la fuerza ficticia. `R_4` es el único punto de corte. Fuente: elaboración propia.

Dado que `(l^2)/(μr^3)` `-` `K/r^2 > 0` entonces (31):

`l_2 > μKr` (31)

La cual proviene de la fuerza ficticia. Por la ecuación de la energía para los puntos de retroceso (17), con `E = E_3` , en (32)

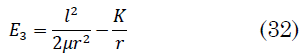
Así que para `l^2= 2μKr`, que es consistente con la restricción `l^2=2μKr`, da `E_3 = 0`. La partícula solo puede aproximarse a una distancia mínima `R_4` del centro de fuerzas (Fig. 6) y la trayectoria de la partícula corresponde a movimiento parabólico.

La región `r< R_4` no es accesible porque la partícula no puede penetrar la región con esos valores de fuerza ficticia; en esta región la velocidad de la partícula toma valores no reales ya que están condicionados por (10), y por la condición (31) que impide que r decrezca de tal forma que no se cumpla la restricción.

Para movimiento parabólico es posible determinar el valor de `F_3 =f´(R_4)` en (33):

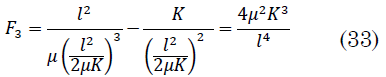
Para otros valores de r que permitan energías `E_4> 0`, la ecuación de la energía da (34):

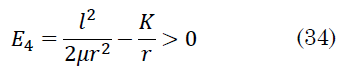
Con la restricción para `l` (35):

`l^2 > 2μKR_4` (35)

Según (36) la fuerza ficticia asociada a `E_4> 0` es:

De acuerdo con la gráfica de fuerza ficticia (Fig. 6), cuando `F’_3` aumenta, la distancia radial se estabiliza en `R_4`. El análisis correcto proviene del hecho de que la fuerza ficticia aumenta debido a que la fuerza real se anula; es decir (37):

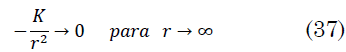
Correspondiendo a la dispersión de la partícula por el centro de fuerzas; por lo tanto, la trayectoria de la partícula es una hipérbola.

    d) `f´(r)_(min) = F_4`. (Fig. 7)

Fig. 7. `f ´(r)_(min) = F_4`. Valor mínimo de la fuerza efectiva. Se obtiene un punto de corte `R_5`. Fuente: elaboración propia.

La condición de mínimo para `f´(r)` es la anulación de su primera derivada dada en (38):

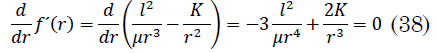
Que permite determinar el punto de corte (39):

Sustituyendo en la ecuación de la fuerza ficticia (40):

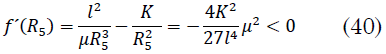
El criterio para determinar la estabilidad de la órbita circular es que (41) [27]:

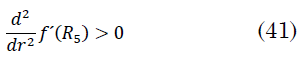
El cálculo del criterio de la segunda derivada conduce a (42):

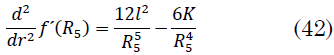
Sustituyendo la condición (39) en (42) nos queda (43):

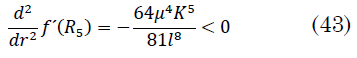
No se verifica la condición de estabilidad; en consecuencia, la solución para el caso d) no es permitida.

En resumen, para el método de la fuerza ficticia, la clasificación de las órbitas según los valores de `f´(r)`, la energía E y el momento angular da los siguientes resultados:

    a) `F_1 = 0`   `E_1 = - K 2Ro < 0`     `l^2 = μKR_0` (circulo)

    b) `F_2< 0`   `E_2 = - K 2a < 0`     `l^2 < μKr` (elipse)

    c) `F_3 > 0`   `E_3= 0`     `l^2 = 2μKr` (parábola)

       `F_3 > 0`   `E_4> 0`     `l^2 = μKr` (Hipérbola)

    d) `F_4 = f’_(min)`   `E_5< 0`     `l^2 < μKr` (no permitida)

En el método de la fuerza ficticia, las restricciones sobre el momento angular `l`, que son consistentes con los valores de la energía `E`, determinan las secciones cónicas.

6. CONCLUSIONES

Se ha elaborado un tratamiento paralelo al método del potencial unidimensional equivalente, para describir las características cualitativas del movimiento de una partícula de masa reducida `μ`, en el caso de fuerza atractiva inversamente proporcional al cuadrado de la distancia. En los círculos académicos la solución a este tipo de movimiento se conoce como el problema de Kepler.

Los dos procedimientos dan los mismos resultados, para el caso del problema de Kepler, en cuando a la clasificación de las posibles trayectorias seguidas por una partícula de masa reducida `μ`. En ambos métodos se utiliza la ecuación de la energía total, que permite la identificación de los puntos de retroceso o distancias absidales.

El método del potencial unidimensional equivalente, para solucionar el problema de Kepler, utiliza la representación gráfica del potencial ficticio con las intersecciones dadas por los posibles valores de la energía total de la partícula. En el símil elaborado por los autores, la forma gráfica de la fuerza ficticia es interceptada por fuerzas arbitrarias, y adicionando la ecuación de la energía de la partícula como complemento para especificar los puntos de retroceso en cada solución.

El mínimo del potencial ficticio proporciona la trayectoria circular para la partícula, mientras en el método de la fuerza ficticia es la igualdad entre la fuerza real y la fuerza `(l^2)/(μr^3)` lo que produce el movimiento circular. La anulación de la energía total en el corte con el potencial ficticio da la órbita parabólica, en tanto que en el método de la fuerza ficticia es el valor específico del momento angular, `l^2 = 2μKr` lo que produce esa cónica. La restricción `l^2 = 2μKr` junto con la condición `E> 0`, dan la órbita hiperbólica en el método de la fuerza ficticia y en el método del potencial ficticio es la restricción `E> 0`, en el corte con el potencial ficticio, lo que genera la órbita hiperbólica.

La órbita elíptica en el método del potencial ficticio se da por la condición de doble corte del potencial ficticio por valores negativos de la energía; igualmente, para el caso de la fuerza ficticia, cuando se tiene el doble corte de la curva `f´(r)` con un valor arbitrario de la fuerza ficticia.

Existen, en cada uno de los casos, soluciones que dan órbitas no permitidas: para el potencial ficticio son los valores de energía `E< 0` por debajo del mínimo del potencial ficticio, y en el caso del método de la fuerza ficticia, los valores de fuerza que están en el mínimo de la curva que producen una órbita circular no estable.

Aunque el método de la fuerza ficticia produce resultados similares al del potencial ficticio, para el problema de Kepler, permite la caracterización de la fuerza ficticia en las diferentes regiones en algunos casos como es el de las trayectorias circular y parabólica. No obstante, el símil requiere una mayor elaboración, siendo el análisis geométrico más complejo.

El método de la fuerza ficticia muestra que las trayectorias no acotadas, parábola e hipérbola, se pueden apreciar más claramente en términos de la intensidad de la fuerza efectiva para el conjunto de valores de `r`. En el caso de las órbitas circulares, el análisis es inmediato, ya que la fuerza `(l^2)/(μr^3)` y la fuerza real toman el mismo valor.

El símil excluye los valores de momento angular nulo, no proporciona secciones cónicas, dado que no se satisfacen las condiciones (21) (órbita circular), (23) (órbita elíptica), (27) (órbita parabólica), (29) (órbita hiperbólica).

Los puntos de retroceso se evalúan a partir de la ecuación de la energía y los puntos de corte son los interceptos de los valores `F_1, F_2, F_3` y `F_4` con `f´(r)`.

Es posible extender el método de la fuerza ficticia para que sea aplicado a otras clases de fuerza central, también tiene su potencialidad en otras áreas de la física, de las ciencias e ingenierías. Para la descripción empírica de la interacción atómica entre moléculas diatómicas, en mecánica cuántica se usa el potencial de Morse que guarda un alto grado de semejanza con la representación gráfica de la fuerza ficticia, línea continua de la Fig. 3. Esta coincidencia abre la posibilidad de aplicar el método de la fuerza ficticia al tratamiento de moléculas diatómicas.

7. AGRADECIMIENTOS

Los autores agradecen a la Vicerrectoría de Investigaciones y Proyección Social de la Universidad Surcolombiana por su apoyo económico para la realización de la presente contribución.

8. REFERENCIAS
9. CONTRIBUCIÓN DE LOS AUTORES

1 Participó activamente en el diseño, conceptualización y desarrollo de la investigación, así como en la elaboración, redacción y revisión final del manuscrito.

2 Participó activamente en el desarrollo de la investigación, elaboración de gráficas, redacción y revisión final del manuscrito.