Recibido: 17 marzo 2020
Aceptado: 10 octubre 2020
Disponible: 13 noviembre 2020

 

---

 

Resumen

La resonancia magnética funcional en estado de reposo (rs-fMRI) es una de las técnicas más relevantes en exploración cerebral. No obstante, la misma es susceptible a muchos factores externos que pueden ocluir la señal de interés. En este orden de ideas, las imágenes rs-fMRI han sido estudiadas desde diferentes enfoques, existiendo un especial interés en las técnicas de eliminación de artefactos a través del Análisis de Componentes Independientes (ICA por sus siglas en inglés). El enfoque es una herramienta poderosa para la separación ciega de fuentes donde es posible eliminar los elementos asociados a ruido. Sin embargo, dicha eliminación está sujeta a la identificación o clasificación de las componentes entregadas por ICA. En ese sentido, esta investigación se centró en encontrar una estrategia alternativa para la clasificación de las componentes independientes. El problema se abordó en dos etapas. En la primera de ellas, se redujeron las componentes (volúmenes 3D) a imágenes mediante el Análisis de Componentes Principales (PCA por sus siglas en inglés) y con la obtención de los planos medios. Los métodos lograron una reducción de hasta dos órdenes de magnitud en peso de los datos y, además, demostraron conservar las características espaciales de las componentes independientes. En la segunda etapa, se usaron las reducciones para entrenar seis modelos de redes neuronales convolucionales. Las redes analizadas alcanzaron precisiones alrededor de 98 % en la clasificación e incluso se encontró una red con una precisión del 98.82 %, lo cual refleja la alta capacidad de discriminación de las redes neuronales convolucionales.

Abstract

Resting state functional magnetic resonance imaging (rs-fMRI) is one of the most relevant techniques in brain exploration. However, it is susceptible to many external factors that can occlude the signal of interest. In this order of ideas, rs-fMRI images have been studied adopting different approaches, with a particular interest in artifact removal techniques through Independent Component Analysis (ICA). Such an approach is a powerful tool for blind source separation, where elements associated with noise can be eliminated. Nevertheless, such removal is subject to the identification or classification of the components provided by the ICA. In that sense, this study focuses on finding an alternative strategy to classify the independent components. The problem was addressed in two stages. In the first one, the components (3D volumes) were reduced to images by Principal Component Analysis (PCA) and by obtaining the median planes. The methods achieved a reduction of up to two orders of magnitude in the weight of the data size, and they were shown to preserve the spatial characteristics of the independent components. In the second stage, the reductions were used to train six models of convolutional neural networks. The networks analyzed in this study reached accuracies around 98 % in classification, one of them even up to 98.82 %, which reflects the high discrimination capacity of convolutional neural networks.

1. INTRODUCCIÓN

---

La neurociencia es un campo científico que se ha abordado desde diferentes perspectivas, no solo con el fin de comprender e interpretar la complejidad del cerebro humano, sino también las fisiopatologías que lo afectan [1]. El interés en esta ciencia ha generado un incremento exponencial en las últimas décadas y, en consecuencia, se han desarrollado múltiples estudios y herramientas de exploración de la actividad cerebral como lo son: la electroencefal2]–[4]. No obstante, esta última es ampliamente utilizada por su carácter no invasivo, por no contar con radiación ionizante y por la alta resolución espacial [5].

Adicionalmente, el enfoque hacia el paradigma en estado de reposo, conocido como resonancia magnética funcional en estado de reposo (rs-fMRI), ha generado buenos resultados en cuanto a detección de circuitos neuronales, como es el caso de la red de modo defecto [6].

Asimismo, la detección de circuitos neuronales ha permitido encontrar y estudiar las diferencias funcionales en patologías tan complejas como el Alzheimer o el Parkinson [7], [8], [9], [10].

La fMRI, y por lo tanto la rs-fMRI, se genera a partir del cambios espontáneos en el nivel de oxigenación en la sangre, conocida como señal BOLD (Blood Oxygen Level Dependent) [11].

Esta señal es una medida indirecta de la actividad neuronal, sin embargo, la fMRI logra captar cambios o ruido de otros procesos que pueden ser de origen fisiológico, instrumental, aleatorio y de movimiento [12]. Por lo tanto, surge la necesidad de limpiar la señal BOLD de todos los elementos o artefactos que ocluyen la señal de interés con el fin de encontrar una resonancia magnética definitiva [13]. En este sentido se han propuesto múltiples métodos, como por ejemplo los de referencia externa, el análisis estadístico sobre la actividad neuronal espontánea [14]–[18] y aplicaciones en aprendizaje de máquina [19]. Adicionalmente, en este último han surgido alternativas prometedoras como el análisis de componentes independientes (ICA). La técnica ha demostrado ser una herramienta poderosa para la separación ciega de fuente, descomponiendo la fMRI en componentes temporales con un mapa espacial asociado [20] (ver Figura 1).

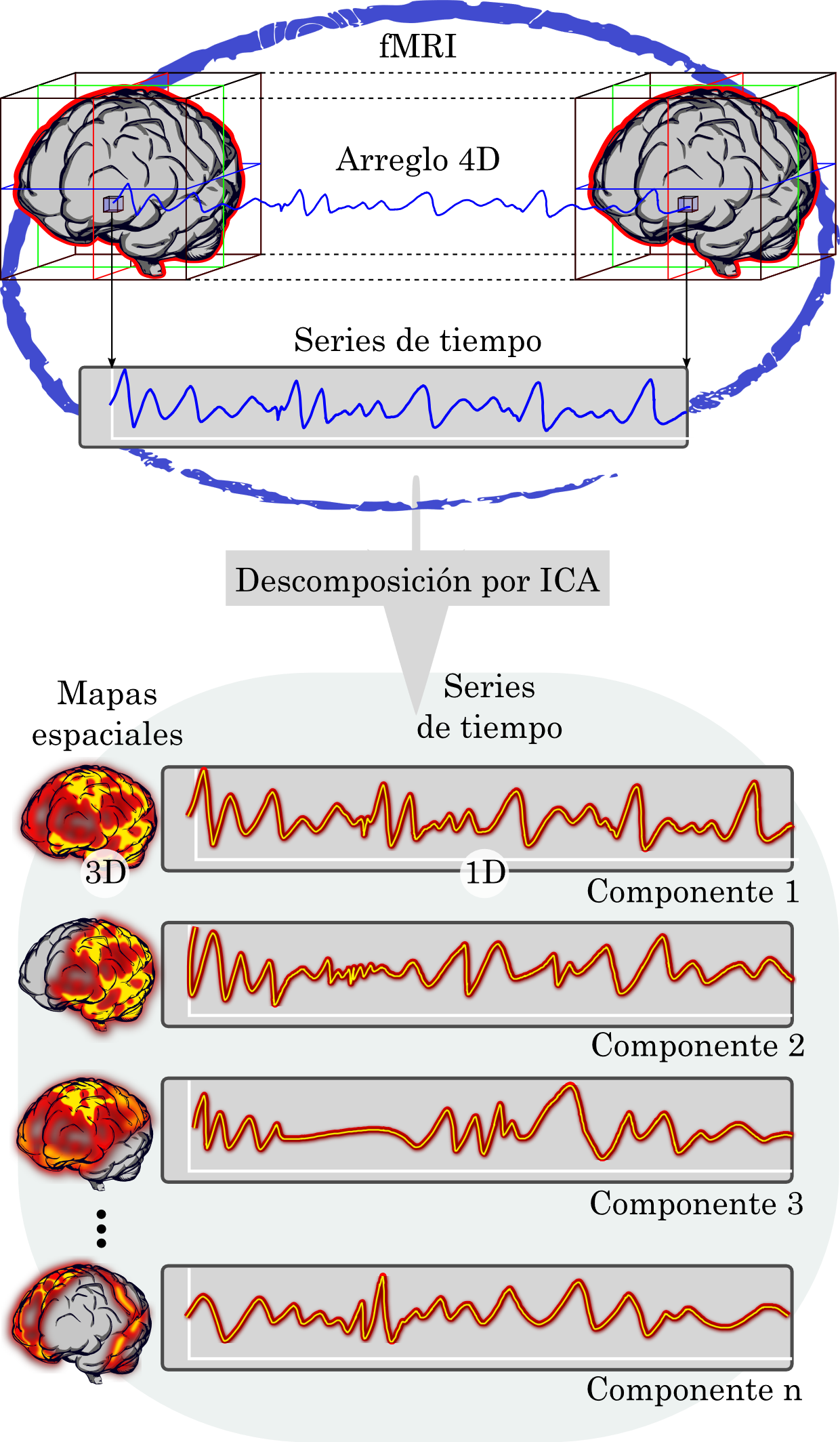
Las características espaciales y temporales de las componentes independientes, permiten discriminarlas entre señal neuronal o ruido, dando paso a una posterior eliminación de los elementos asociados al ruido 20], [21]. No obstante, la clasificación no se presenta como una tarea sencilla, ya que requiere de experiencia y se puede tornar en una tarea tediosa debido a la cantidad de componentes generados [22].

La clasificación ha impulsado estrategias automáticas como ICA-AROMA [21] o ICA-FIX [23], [24]. Estas se basan en discriminar las componentes a partir de las características temporales, espectrales y/o espaciales. Sin embargo, la eliminación de artefactos, mediante la clasificación manual, aún sigue siendo el estándar de oro. Incluso, la validación de métodos automatizados se fundamenta en comparar los resultados con la clasificación manual. Más aún, la existencia de componentes inusuales requieren de una compresión detallada del tema, a fin de clasificarlas correctamente [22].

Por otro lado, las redes neuronales convolucionales y el aprendizaje profundo son algunos de los temas de mayor crecimiento en informática médica [25]. Las redes pueden ser entrenadas con datos puros o con características extraídas manualmente. Asimismo, la flexibilidad de estas les ha permitido estar inmersas en diferentes áreas e incluso es posible hacer adaptaciones entre dominios [26].

Además, las aplicaciones más comunes han superado las técnicas convencionales de aprendizaje de máquina en áreas como: reconocimiento de patrones, detección, visión por computadora y clasificación [27]. Incluso, en esta última tarea se ha logrado superar el rendimiento humano [28]. De hecho, el interés en el aprendizaje profundo y su multidisciplinariedad, ha permitido el desarrollo de estrategias sobre el análisis de las imágenes de resonancia magnética [29]–[33]. Por ejemplo, en la clasificación de trastornos bajo el paradigma en estado de reposo [29].

En este sentido, son claras las ventajas manifestadas por el aprendizaje profundo [34], limitado únicamente por el número de datos necesarios para entrenar los algoritmos, los cuales pueden estar en el orden de los miles de datos. En consecuencia, esto se presenta como una carga computacional muy elevada, más aún en el caso de las rs-fMRI, donde los datos son arreglos de cuatro dimensiones que superan el peso de una imagen convencional.

Partiendo de las anteriores consideraciones, este estudio tiene dos enfoques principales. El primero de ellos está orientado a buscar la mejor forma de representar las componentes independientes. Este problema se aborda con algunas técnicas ya existentes, como la reducción de dimensiones mediante el análisis de componentes principales (PCA) [35] y la visualización por cortes axiales. En el segundo enfoque, se busca encontrar una solución de alta precisión para la detección de artefactos (ruido), utilizando los mapas espaciales extraídos del análisis de componentes independientes sobre imágenes de resonancia magnética funcional en estado de reposo. Este último se afronta desde las redes neuronales convolucionales (CNN) [36] con el diseño de seis tipos de redes e implementadas sobre las previas representaciones de las componentes independientes.

2. MATERIALES Y MÉTODOS

---

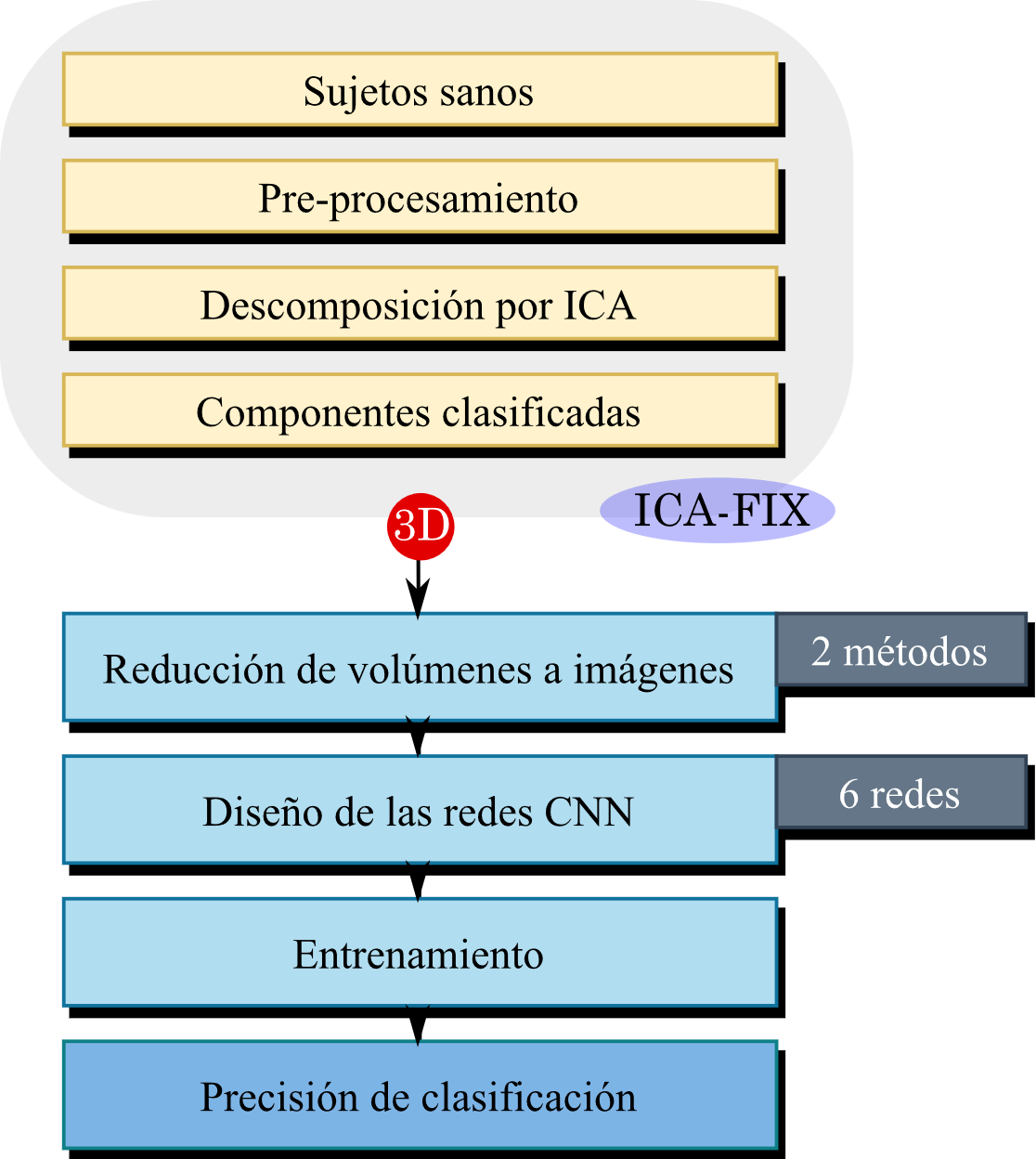
En la Figura 2 se proporciona una descripción general de la estrategia seguida. En el proceso se usó una base de datos de acceso público, la cual cuenta con el preprocesamiento mínimo [37], la descomposición mediante ICA y la respectiva clasificación. Posteriormente, los métodos de reducción se aplicaron a las componentes (volúmenes 3D) y, con las imágenes generadas, se entrenaron las diferentes redes neuronales. Finalmente, las redes se validaron calculando la precisión de clasificación.

2.1 Componentes independientes

Se usó la base de datos pública del proyecto ICA-FIX. El conjunto se basa en 6 grupos de imágenes rs-fMRI obtenidas de los proyectos Human Connectome Project [38] y Whitehall II imaging study [39].Los datos cuentan con la descomposición ICA realizada con el software FSL-5.0 [40], [41]. Asimismo, esta se implementó con la herramienta llamada descomposición optimizada lineal exploratoria multivariada en componentes independientes (MELODIC por su siglas en inglés) [23], [24], [42]. Se usaron en total 13951 componentes independientes, de las cuales 2831 están etiquetadas como señal (actividad neuronal) y 11120 como ruido.

La clasificación fue realizada por los expertos de ICA-FIX [43], usando las características espaciales, temporales y frecuenciales [22]. En Tabla 1 se muestra el resumen de los datos obtenidos.

Cabe resaltar que, aunque la descomposición por ICA genera mapas espaciales y series de tiempos, en este proceso solo se incluyeron los mapas espaciales. Por lo tanto, los métodos descritos a continuación se aplicaron únicamente a estos conjuntos de componentes 3D.

Además, los datos pueden ser descargados directamente de la página oficial en el siguiente enlace (https://www.fmrib.ox.ac.uk/datasets/FIX-training/).

2.2 Reducción de volúmenes

Los volúmenes de las componentes se redujeron a imágenes mediante el análisis de componentes principales (PCA) y tomando los cortes medios. Los métodos se describen con detalle a continuación.

Método 1- Reducción de volúmenes por PCA: Se implementó el análisis de componentes principales para obtener tres imágenes equivalentes a los cortes axial, coronal y sagital. La imagen axial se generó dividiendo el volumen en cortes axiales como se muestra en la Figura 3. Cada corte se consideró como una matriz de observaciones con `p×q` variables, donde `p` y `q` y son los tamaños del volumen en los ejes coronal y sagital respectivamente.

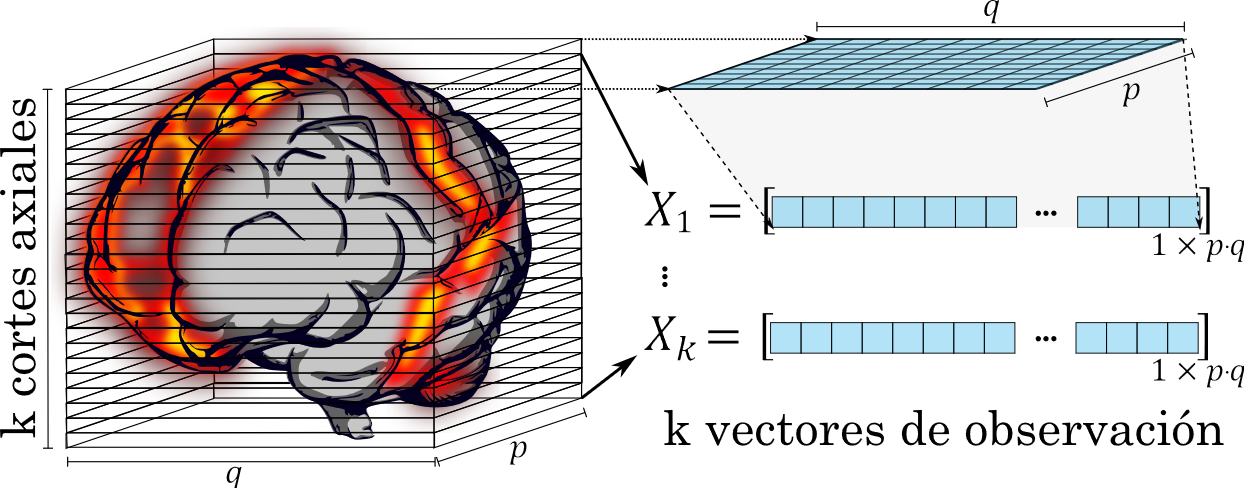
Posteriormente, cada matriz se almacenó en un vector `X_i` correspondiente al i-ésimo corte con dimensiones equivalentes a las dimensiones `p∙q` (ver Figura 3).

Con estos vectores es posible encontrar las componentes principales, considerando que estas se generan como una combinación lineal de los k vectores originales, es decir, la primera componente principal es equivalente a (1):

Donde `u_11` hasta `u_1k` son escalares que se calculan a partir de la máxima varianza de `z_1`.

Las componentes principales subsecuentes se definen de manera similar. Sin embargo, los coeficientes `u` se calculan a partir de la máxima varianza y considerando que cada una debe tener covarianza cero con la anterior componente [35].

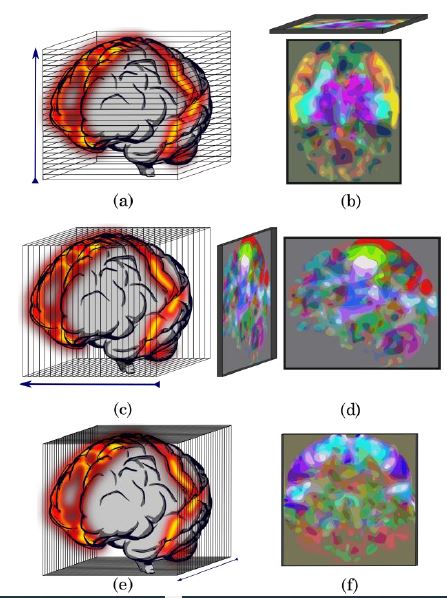
En (1) se puede ver que las componentes principales tienen las mismas dimensiones de los vectores `X_i` Por lo tanto, a cada componente se les puede aplicar el proceso inverso ilustrado en la Figura 3. El proceso genera matrices de tamaño `p×q` y las tres primeras componentes principales se almacenan en los canales RGB para generar la imagen estándar de 8 bits (ver Figura 4 (b). Las imágenes de los cortes coronal y sagital se generan de la misma manera, sin embargo, las matrices de observaciones se toman como los cortes consecutivos a lo largo de sus respectivos ejes como se ilustra en la Figura 4 (c) y (e), obteniéndose imágenes similares a las ilustradas en la Figura 4 (d) y (f).

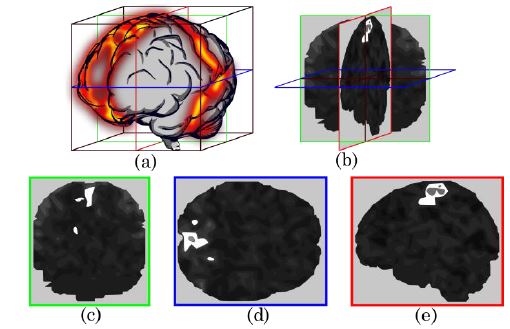
Método 2 – Reducción de volúmenes en tres cortes perpendiculares: cada volumen se redujo a tres imágenes correspondientes a los cortes medios en los planos axial, coronal y sagital.

La Figura 5 muestra una ilustración de los planos tomados en cada volumen. Adicionalmente, a las imágenes se les realizó un ajuste en los niveles de gris mediante la modificación del histograma. Se ajustó la intensidad tomando 2 como el mínimo y 22 como el máximo, es decir, los niveles entre 2 a 22 se ajustaron proporcionalmente a una escala de 0 a 255 para generar la imagen de 8 bits.

La reducción se realizó sobre la plataforma Colab de Google, utilizando el lenguaje de programación Python. Además, se usaron principalmente las librerías de Nibabel, Numpy y Opencv.

2.3 Diseño de las redes neuronales convolucionales

Debido a la versatilidad y flexibilidad de las redes, se optó por diseñar seis redes neuronales convolucionales crecientes [44]. Los modelos de las redes se implementaron bajo las siguientes características:

-Función de pérdida de sparse categorical crossentropy.

-Optimizador Adam basado en un gradiente de primer orden estocástico.

-Regularizaron mediante la técnica de deserción de neuronas o dropout.

-Función de activación softmax en la capa de salida.

Haciendo uso de una función lambda, las imágenes se normalizan a la entrada de las redes. Posteriormente, se agregaron las capas convolucionales en combinación con las de submuestreo. Las salidas de las convolucionales se aplanaron, se pasaron a la estructura de capas densa y se redujeron gradualmente hasta la capa de dos salidas (clasificador binario). Las redes difieren en el número de capas convolucionales, la cantidad de filtros, el número de capas densas y el número de perceptrones. En la Tabla 2 se muestra detalladamente las estructuras de los modelos. Cabe señalar que el último modelo tiene la estructura de la red LeNet-5 [45], la cual sigue el mismo comportamiento de las cinco primeras.

Nuevamente, el diseño de las redes neuronales convolucionales se generó en la plataforma Colab con las librerías de Keras y TensorFlow.

2.4 Entrenamiento

El entrenamiento de las redes se realizó con el 80 % de los datos (datos de entrenamiento). Es decir, se usaron las reducciones de 11161 componentes independientes, las cuales se seleccionaron aleatoriamente. Durante el entrenamiento se implementó la validación cruzada, ajustando los parámetros de la red con el 90 % de los datos de entrenamiento y validando con 10 % restante. La técnica toma las particiones aleatoriamente en cada época y al final valida calculando la precisión de clasificación. Por otro lado, el entrenamiento se ejecutó con un tamaño de lote de 16 muestras y 50 épocas de entrenamiento, a fin de alcanzar la máxima precisión [46].

Los seis modelos se entrenaron con cada conjunto de las tres imágenes generadas por los dos métodos. Además, el proceso se repitió 15 veces y los resultados se almacenaron automáticamente con la función ModelCheckpoint. Finalmente, el desempeño de los modelos se observó mediante la precisión de la validación cruzada (datos de entrenamiento) y con los datos de prueba. Para esta última, se usó el 20 % de los datos restantes, es decir, las 2790 componentes independientes ajenas al entrenamiento a fin de evitar el sobreajuste. Cabe aclarar que, la medida de precisión es el número de aciertos totales sobre el número total de elementos predichos. En otras palabras, es la métrica conocida en aprendizaje de máquina como accuracy [47].

3. RESULTADOS

---

3.1 Reducción de volúmenes

Se redujeron 13951 volúmenes de las componentes independientes (ver Tabla 1). A cada volumen se le encontraron las representaciones de los cortes axial, coronal y sagital mediante los dos métodos descritos. En la Tabla 3 se muestran los pesos promedios de las componentes por volúmenes y las reducciones a imágenes, donde es notoria la reducción hasta en dos órdenes de magnitud.

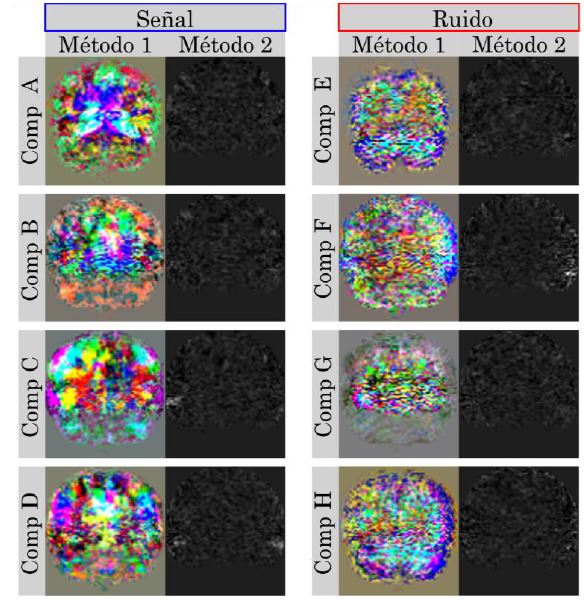
En la Figura 6 se muestran ocho componentes independientes, cuatro asociadas a actividad neuronal (señal) y cuatro a ruido. Los dos métodos arrojaron imágenes similares con características que se presentan en las mismas regiones anatómicas. Es decir, donde se espera que la componente esté ubicada. Por otro lado, el método 2 es el mapa espacial real de la componente de un único corte (corte medio). Por lo tanto, gracias a la concordancia espacial de las dos imágenes, se puede inferir que el primer método está conservando parte de las características espaciales. Por ejemplo, la componente A en el método 2 indica que esta se ubica en la parte posterior del cerebro, región que se resalta en el primer método. De hecho, los colores de esta región presentan mayor homogeneidad en contraste con la irregularidad de las otras regiones. Por otra parte, las imágenes relacionadas con el ruido no presentan regiones homogéneas tan definidas, lo cual supone una diferencia entre estos dos tipos de componentes independientes.

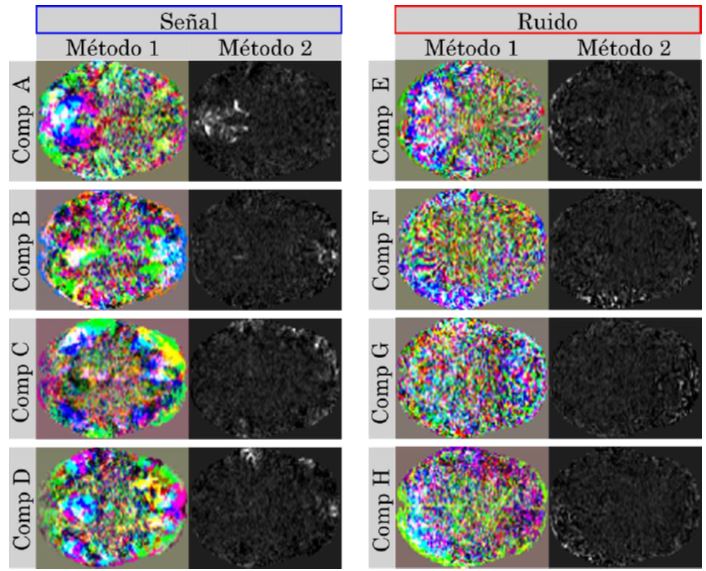
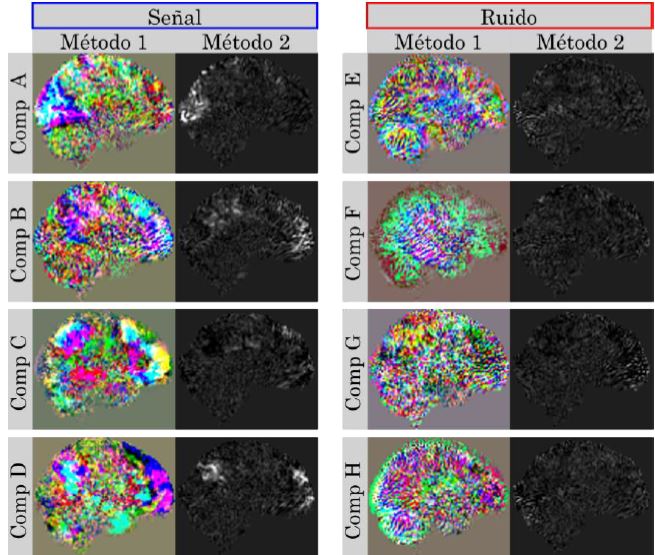
En la Figura 7 y Figura 8 se muestran las imágenes coronales y sagitales de las mismas ocho componentes independientes. En estas imágenes se presenta un comportamiento similar. Las regiones sobresalen con alguna característica especial, donde se esperaría encontrar la componente. Además, estas regiones concuerdan con la posición espacial respecto a las imágenes axiales. Por ejemplo, la componen A en la Figura 6 se presenta en la parte posterior del cerebro al igual que en la imagen sagital de la Figura 8. Asimismo, en la Figura 7 y Figura 8, las componentes asociadas a ruido presentan un comportamiento irregular respecto a las componentes de actividad neuronal (señal).

3.2 Entrenamiento

El entrenamiento de los seis modelos, los tres conjuntos de imágenes y los dos métodos, generaron 36 posibles combinaciones como se muestra en la Tabla 4. En esta, se registró la precisión máxima alcanzada por los datos de prueba, la cual abarcó valores entre 0.8958 hasta 0.9882. Cabe resaltar que el valor máximo fue entregado por el método de reducción por PCA con el modelo 6 y sobre la imagen coronal.

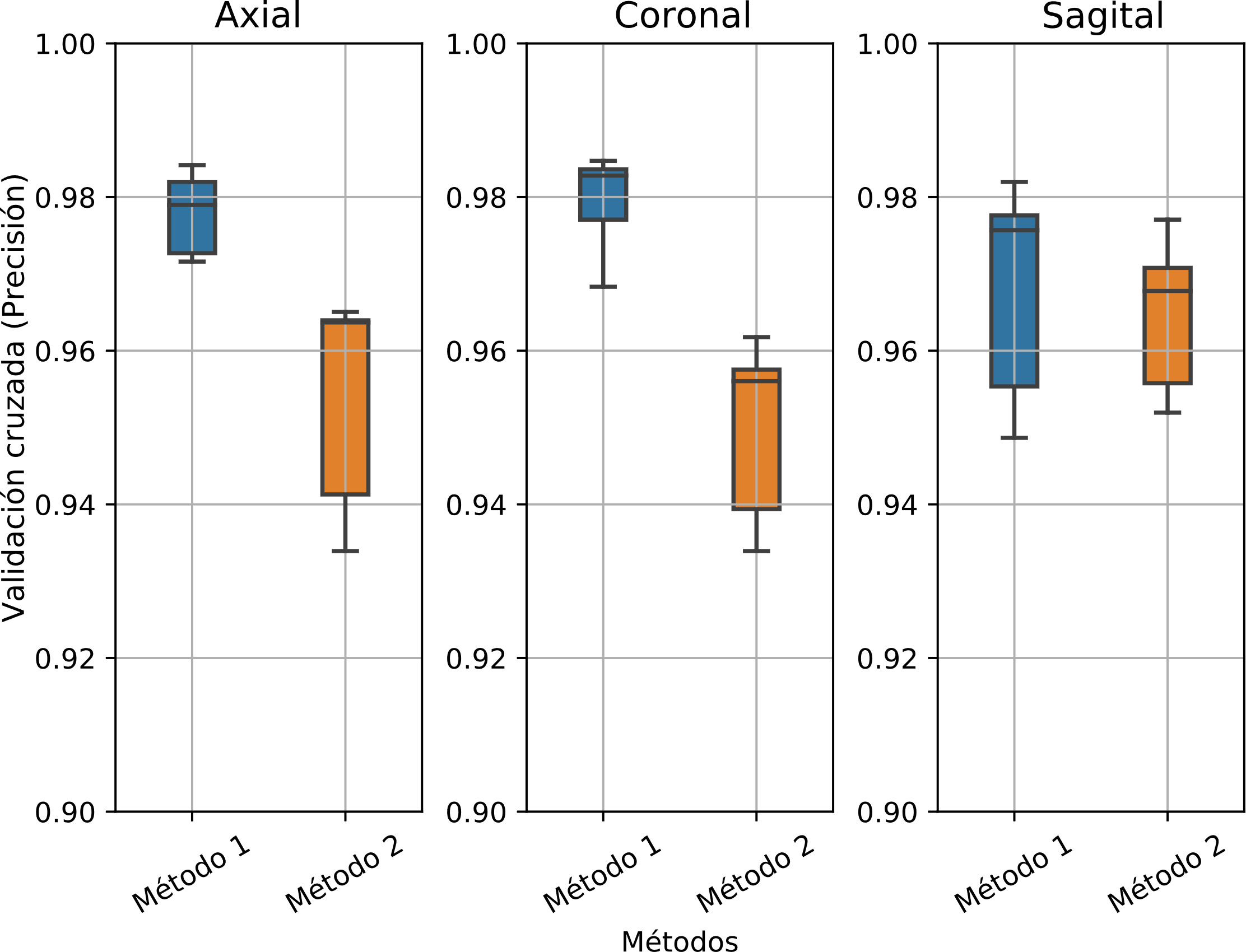
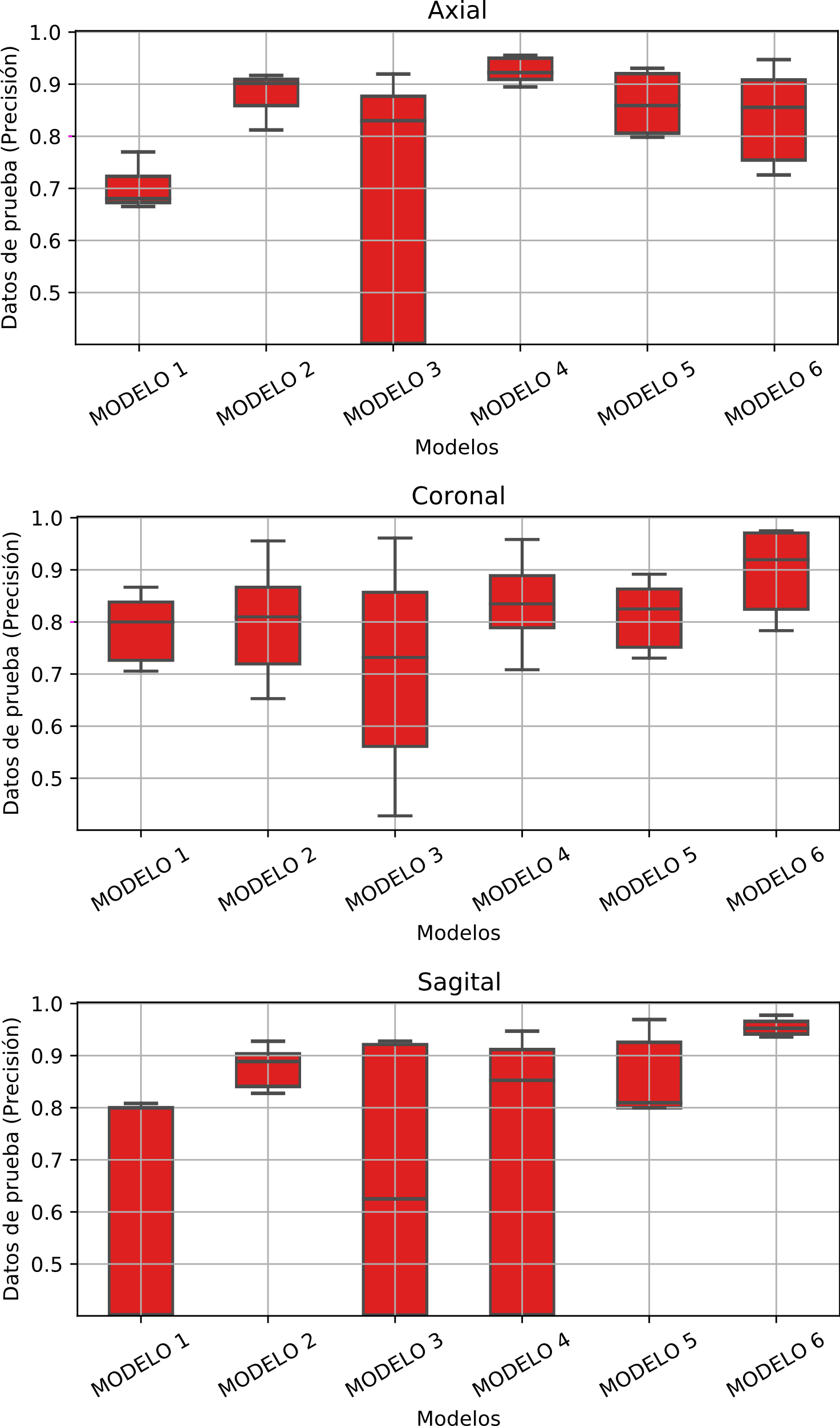
La Figura 9, Figura 10, Figura 11, ilustran el comportamiento de la precisión, producto de los 15 entrenamientos, frente a los métodos y modelos implementados.

La Figura 9 muestra la distribución para la validación cruzada. En las tres gráficas se ilustra el comportamiento de las imágenes axial, coronal y sagital, respectivamente. En ellas se ve claramente que el método 1 tuvo mejores resultados para las imágenes axial y coronal. Por el contrario, la distribución en la imagen sagital tuvo un comportamiento similar entre los dos métodos.

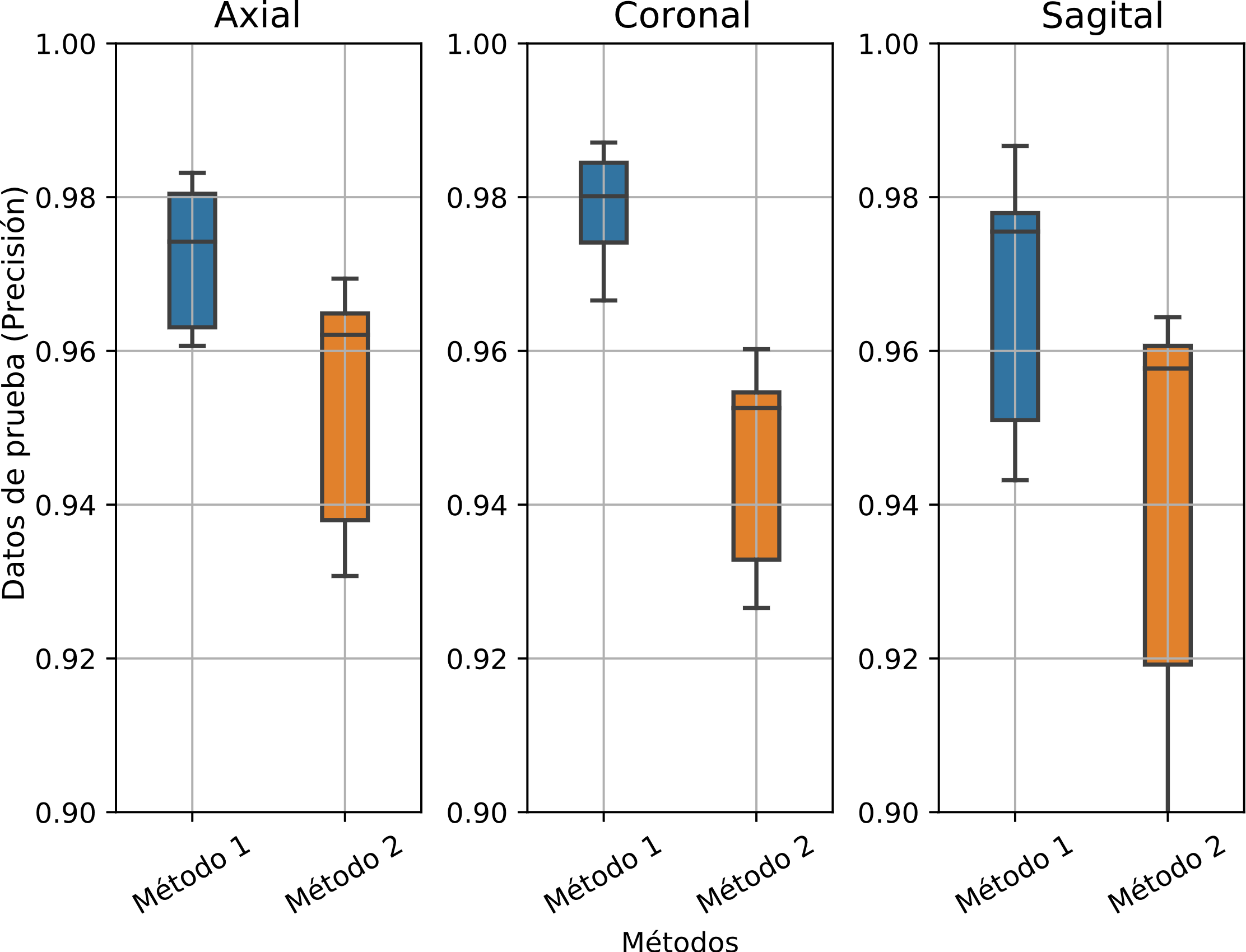
Análogo al caso anterior, la Figura 10 muestra la distribución para los datos de prueba.

En las tres gráficas se ilustra el comportamiento de las imágenes axial, coronal y sagital, respectivamente. En ellas se ve nuevamente que el método 1 tuvo mejores resultados para las imágenes axial y coronal. Por el contrario, la distribución en las imágenes sagitales no tuvo la misma distinción de las dos anteriores.

La Figura 10 muestra la distribución de los datos de prueba en función de los modelos. En las tres gráficas se ilustra el comportamiento de las imágenes axial, coronal y sagital respectivamente. En estas se ve que el modelo 3 tuvo la peor distribución en todos los casos.

Por otro lado, el modelo 6 con la imagen sagital tuvo una distribución más compacta y alta, concentrándose por encima de 0.9. Finalmente, la imagen coronal tuvo un comportamiento más homogéneo entre los modelos, a excepción del modelo 3. Incluso, esta imagen y el modelo 6 generaron la precisión más alta (ver Tabla 4), además, su distribución se mantuvo por encima de 0.8.

4. DISCUSIÓN

---

La clasificación de los artefactos, mediante el análisis de componentes independientes, es un tema relevante en la limpieza de las imágenes de resonancia magnética funcional en estado de reposo. La técnica ha impulsado el desarrollo de estrategias estadísticas, matemáticas, de inteligencia artificial y de aprendizaje automático. Claros ejemplos de esto son ICA-AROMA e ICA-FIX [33], herramientas que están a la vanguardia en términos de clasificación y eliminación de artefactos. De hecho, estas cuentan con precisiones del 92 % al 99 %. No obstante, hoy en día existen técnicas prometedoras en el aprendizaje profundo como las redes neuronales convolucionales, las cual ha demostrado superar la capacidad humana en la clasificación [28].

En este sentido, nosotros propusimos una nueva estrategia de dos etapas para la clasificación de componentes independientes. En la primera etapa, se redujeron los volúmenes de las componentes independientes a imágenes a través de dos métodos diferentes. En la segunda, las reducciones se usaron sobre seis redes neuronales convolucionales a fin de entrenar los mejores modelos de clasificación.

En primer lugar, los dos métodos de reducciones tuvieron una disminución de hasta dos órdenes de magnitud, lo cual supone una reducción en la carga computacional sobre la cantidad de datos necesarios en el aprendizaje profundo [48]. Adicionalmente, la reducción por PCA (primer método), mostró ser una técnica robusta para la clasificación de componentes independientes. Asimismo, fue posible observar que la combinación de las reducciones con las redes neuronales convolucionales superó la precisión de clasificación de ICA-AROMA [21].

Por otro lado, todas las redes neuronales convolucionales alcanzaron precisiones de clasificación del 89.59 al 98.82 %, valores muy cercanos al 99 % alcanzado por ICA-FIX [23].

Además, gracias a los valores altos en la precisión, el enfoque hacia las redes neuronales convolucionales se muestra como una técnica prometedora. Incluso, dando paso a la posibilidad de encontrar una red más eficiente que pueda superar el 99 % producido por ICA-FIX [23].

5. CONCLUSIONES

---

Hemos estudiado dos métodos de reducción o representación de los volúmenes de componentes independientes de imágenes de resonancia magnética funcional en estado de reposo. Estos demostraron ser eficientes en cuanto a reducción y conservación de las características espaciales de las componentes independientes. Las reducciones se combinaron con seis redes neuronales convolucionales, a fin de crear modelos de clasificación automática, en donde se alcanzaron precisiones cercanas al 98 % de clasificación. Incluso, se halló una red con una precisión del 98.82 %, superando el poder de clasificación de la mayoría de los métodos de clasificación basados en aprendizaje de máquina.

6. AGRADECIMIENTOS

---

Este trabajo fue apoyado por el Departamento Administrativo de Ciencias, Tecnología e Innovación (Colciencias) por el proyecto ‘Identificación de Biomarcadores Preclínicos en Enfermedad de Alzheimer a través de un Seguimiento Longitudinal de la Actividad Eléctrica Cerebral en Poblaciones con Riesgo Genético’, código 111577757635. Este artículo no contó con financiación económica.

CONFLICTOS DE INTERÉS DE LOS AUTORES

---

Los autores declaran no tener ningún conflicto de interés.

CONTRIBUCIÓN DE LOS AUTORES

---

Leonel Mera-Jiménez: conceptualización del modelo; diseño e implementación del código computacional; diseño, ejecución y validación de experimentos; preparación del documento borrador original; revisión, edición y aprobación del documento final.

John F. Ochoa-Gómez: conceptualización del modelo; validación de experimentos y código computacional; revisión, edición y aprobación del documento final.

7. REFERENCIAS

---

• arrow_upward [1]   G. A. Ascoli; M. Halavi, “Neuroinformatics,” Encyclopedia of Neuroscience. pp. 477–484, 2009. https://doi.org/10.1016/B978-008045046-9.00872-X
• arrow_upward [2]   P. M. Rossini et al., “Methods for analysis of brain connectivity: An IFCN-sponsored review,” Clinical Neurophysiology, vol. 130, no. 10, pp. 1833–1858, Oct. 2019. https://doi.org/10.1016/j.clinph.2019.06.006
• arrow_upward [3]   L. A. Muñoz-Bedoya; L. E. Mendoza; J. Velandia-Villamizar, “Segmentation of Magnetic Resonance Imaging MRI using LS-SVM and Wavelet Multiresolution Analysis,” TecnoLógicas, edición especial, pp. 681-693, Oct. 2013. https://doi.org/10.22430/22565337.381
• arrow_upward [4]   C. Guarnizo-Lemus, “Análisis de reducción de ruido en señales EEG orientado al reconocimiento de patrones,” TecnoLógicas, no. 21, pp. 67-80, Dec. 2008. https://doi.org/10.22430/22565337.248
• arrow_upward [5]   J. L. Armony; D. Trejo Martínez; D. Hernández, “Resonancia Magnética Funcional (RMf): principios y aplicaciones en Neuropsicología y Neurociencias Cognitivas,” Rev. Neuropsicol. Latinoam., vol. 4, no. 2, pp. 36–50, Apr. 2012. https://www.neuropsicolatina.org/index.php/Neuropsicologia_Latinoamericana/article/view/103
• arrow_upward [6]   M. E. Raichle, “The Brain’s Default Mode Network,” Annu. Rev. Neurosci., vol. 38, pp. 433–447, May. 2015. https://doi.org/10.1146/annurev-neuro-071013-014030
• arrow_upward [7]   W. Qian et al., “Delusions in Alzheimer Disease are Associated with Decreased Default Mode Network Functional Connectivity,” Am. J. Geriatr. Psychiatry, vol. 27, no. 10, pp. 1060–1068, Oct. 2019. https://doi.org/10.1016/j.jagp.2019.03.020
• arrow_upward [8]   R. Franciotti et al., “Somatic symptoms disorders in Parkinson’s disease are related to default mode and salience network dysfunction,” NeuroImage Clin., vol. 23, Apr. 2019. https://doi.org/10.1016/j.nicl.2019.101932
• arrow_upward [9]   S. Lang; N. Duncan; G. Northoff, “Resting-state functional magnetic resonance imaging: Review of neurosurgical applications,” Neurosurgery, vol. 74, no. 5. pp. 453–464, Jan. 2014. https://doi.org/10.1227/NEU.0000000000000307
• arrow_upward [10] G. D. Pearlson, “Applications of Resting State Functional MR Imaging to Neuropsychiatric Diseases,” Neuroimaging Clin N. Am., vol. 27, no. 4, pp. 709–723, Nov. 2017. https://doi.org/10.1016/j.nic.2017.06.005
• arrow_upward [11] J. D. Kropotov, “Functional Magnetic Resonance Imaging,” in Functional Neuromarkers for Psychiatry applications for diagnosis and treatment, Elsevier inc., 2016, pp. 17–25. https://doi.org/10.1016/B978-0-12-410513-3.00003-6
• arrow_upward [12] J. Mohan; V. Krishnaveni; Y. Guo, “A survey on the magnetic resonance image denoising methods,” Biomed. Signal Process, vol. 9, no. 1, pp. 56–69, Jan. 2014. https://doi.org/10.1016/j.bspc.2013.10.007
• arrow_upward [13] L. L. Wald, “Ultimate MRI,” J. Magn. Reson., vol. 306, pp. 139–144, Sep. 2019. https://doi.org/10.1016/j.jmr.2019.07.016
• arrow_upward [14] D. S. Margulies et al., “Resting developments: A review of fMRI post-processing methodologies for spontaneous brain activity,” Magn. Reson. Mater. Physics, Biol. Med., vol. 23, no. 5–6, pp. 289–307, Oct. 2010. https://doi.org/10.1007/s10334-010-0228-5
• arrow_upward [15] M. A. Lindquist, “The Statistical Analysis of fMRI Data,” Statistical Science., vol. 23, no. 4, pp. 439–464, 2008. http://dx.doi.org/10.1214/09-STS282
• arrow_upward [16] K. Chen; A. Azeez; D. Y. Chen; B. B. Biswal, “Resting-state Functional Connectivity: Signal Origins and Analytic Methos,” Neuroimag Clin N. Am, vol. 30, no. 1, pp. 15–23, Feb. 2020. https://doi.org/10.1016/j.nic.2019.09.012
• arrow_upward [17] F. Gregory Ashby, Statistical Analysis of fMRI Data, Second. MIT press. 2019. https://doi.org/10.7551/mitpress/11557.001.0001
• arrow_upward [18] M. M. Monti, “Statistical analysis of fMRI time-series: a critical review of the GLM approach,” in Front. Hum. Neurosci, vol. 5, no. 28, pp. 147–154. Mar. 2011. https://doi.org/10.3389/fnhum.2011.00028
• arrow_upward [19] M. Khosla; K. Jamison; G. H. Ngo; A. Kuceyeski; M. R. Sabuncu, “Machine learning in resting-state fMRI analysis,” Magnetic Resonance Imaging, vol. 64, pp. 101–121, Dec. 2019. https://doi.org/10.1016/j.mri.2019.05.031
• arrow_upward [20] C. F. Beckmann, M. DeLuca, J. T. Devlin; S. M. Smith, “Investigations into resting-state connectivity using independent component analysis,” Philos. Trans. R. Soc. B Biol. Sci., vol. 360, no. 1457, pp. 1001–1013, May. 2005. https://doi.org/10.1098/rstb.2005.1634
• arrow_upward [21] R. H. R. Pruim; M. Mennes; D. Van Rooij; A. Llera; J. K. Buitelaar; C. F. Beckmann, “ICA-AROMA : A robust ICA-based strategy for removing motion artifacts from fMRI data,” Neuroimage, vol. 112, pp. 267–277, May. 2015. https://doi.org/10.1016/j.neuroimage.2015.02.064
• arrow_upward [22] L. Griffanti et al., “Hand classification of fMRI ICA noise components,” Neuroimage, vol. 154, pp. 188–205, Jul. 2017. https://doi.org/10.1016/j.neuroimage.2016.12.036
• arrow_upward [23] L. Griffanti et al., “ICA-based artefact removal and accelerated fMRI acquisition for improved resting state network imaging,” Neuroimage, vol. 95, pp. 232–247, Jul. 2014. https://doi.org/10.1016/j.neuroimage.2014.03.034
• arrow_upward [24] G. Salimi-Khorshidi; G. Douaud; C. F. Beckmann; M. F. Glasser; L. Griffanti; S. M. Smith, “Automatic denoising of functional MRI data: Combining independent component analysis and hierarchical fusion of classifiers,” Neuroimage, vol. 90, pp. 449–468, Apr. 2014, https://doi.org/10.1016/j.neuroimage.2013.11.046
• arrow_upward [25] D. Ravi et al., “Deep Learning for Health Informatics,” IEEE J. Biomed. Heal. Informatics, vol. 21, no. 1, pp. 4–21, Jan. 2017. https://doi.org/10.1109/JBHI.2016.2636665
• arrow_upward [26] J. A. Peña-Torres; R. E. Gutiérrez; V. A. Bucheli; F. A. González, “Cómo adaptar un modelo de aprendizaje profundo a un nuevo dominio: el caso de la extracción de relaciones biomédicas,” TecnoLógicas, vol. 22, Edición especial, pp. 49–62, Dic. 2019. http://dx.doi.org/10.22430/22565337.1483
• arrow_upward [27] W. Liu; Z. Wang; X. Liu; N. Zeng; Y. Liu; F. E. Alsaadi, “A survey of deep neural network architectures and their applications,” Neurocomputing, vol. 234, no. 19, pp. 11–26, Apr. 2017. https://doi.org/10.1016/j.neucom.2016.12.038
• arrow_upward [28] K. He; X. Zhang; S. Ren; J. Sun, “Delving deep into rectifiers: Surpassing human-level performance on imagenet classification,” in Proceedings of the IEEE International Conference on Computer Vision, 2015, Santiago de chile, 2015. pp. 1026–1034. https://doi.org/10.1109/ICCV.2015.123
• arrow_upward [29] Z. Mao et al., “Spatio-temporal deep learning method for ADHD fMRI classification,” Inf. Sci., vol. 499, pp. 1–11, Oct. 2019. https://doi.org/10.1016/j.ins.2019.05.043
• arrow_upward [30] A. Riaz; M. Asad; E. Alonso; G. Slabaugh, “DeepFMRI: End-to-end deep learning for functional connectivity and classification of ADHD using fMRI,” J. Neurosci. Methods, vol. 335, p. 108506, Apr. 2020. https://doi.org/10.1016/j.jneumeth.2019.108506
• arrow_upward [31] M. P. Hosseini; T. X. Tran; D. Pompili; K. Elisevich; H. Soltanian-Zadeh, “Multimodal data analysis of epileptic EEG and rs-fMRI via deep learning and edge computing,” Artif. Intell. Med., vol. 104, Apr. 2020. https://doi.org/10.1016/j.artmed.2020.101813
• arrow_upward [32] A. S. Lundervold; A. Lundervold, “An overview of deep learning in medical imaging focusing on MRI,” Zeitschrift fßr Medizinische Phys., vol. 29, no. 2, pp. 102–127, May. 2019. https://doi.org/10.1016/j.zemedi.2018.11.002
• arrow_upward [33] M. Mostapha; M. Styner, “Role of deep learning in infant brain MRI analysis,” Magnetic Resonance Imaging, vol. 64, pp. 171–189, Dec. 2019. https://doi.org/10.1016/j.mri.2019.06.009
• arrow_upward [34] Y. Guo; Y. Liu, A. Oerlemans; S. Lao; S. Wu; M. S. Lew, “Deep learning for visual understanding: A review,” Neurocomputing, vol. 187, pp. 27–48, Apr. 2016. https://doi.org/10.1016/j.neucom.2015.09.116
• arrow_upward [35] W. Hernandez; A. Mendez, “Application of Principal Component Analysis to Image Compression,” in Statistics - Growing Data Sets and Growing Demand for Statistics, Türkmen Gö., 2018. http://dx.doi.org/10.5772/intechopen.75007
• arrow_upward [36] J. Teuwen; N. Moriakova, “Convolutional neural networks,” in Handbook of Medical Image Computing and Computer Assisted Intervention, Academic P., Ed. 2020, pp. 481–501. https://doi.org/10.1016/B978-0-12-816176-0.00025-9
• arrow_upward [37] M. F. Glasser et al., “The minimal preprocessing pipelines for the Human Connectome Project,” Neuroimage, vol. 80, pp. 105–124, Oct. 2013. https://doi.org/10.1016/j.neuroimage.2013.04.127
• arrow_upward [38] T. H. C. Projet, “HCP Young Adult - Connectome – Publications an overview,” 2009. https://www.humanconnectome.org/study/hcp-young-adult
• arrow_upward [39] Department of Psychiatry, Warneford Hospital, Oxford, OX3 7JX “Whitehall Imaging Oxford” https://www.psych.ox.ac.uk/research/neurobiology-of-ageing/research-projects-1/whitehall-oxford
• arrow_upward [40] “FMRIB Software Library v6.0,” Created by the Analysis Group, FMRIB, Oxford, UK. 2020. https://fsl.fmrib.ox.ac.uk/fsl/fslwiki
• arrow_upward [41] M. Jekinson; C. F. Beckmann; T. E. J. Behrens; M. W. Woolrich; S. M. Smith, “FSL,” Neuroimage, vol. 62, no. 2, pp. 782–790, Aug. 2012. https://doi.org/10.1016/j.neuroimage.2011.09.015
• arrow_upward [42] The Analysis Group FMRIB, “MELODIC.”, version 3.04, 2019. https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/MELODIC
• arrow_upward [43] G. Salimi-khorshidi et al., “Fix Hand-Training Datasets.” https://www.fmrib.ox.ac.uk/datasets/FIX-training/
• arrow_upward [44] S. M. Anwar; M. Majid; A. Qayyum; M. Awais; M. Alnowami; M. K. Khan, “Medical Image Analysis using Convolutional Neural Networks: A Review,” Journal of Medical Systems, vol. 42, no. 11, pp. 1–13, 2018. https://doi.org/10.1007/s10916-018-1088-1
• arrow_upward [45] Y. LeCun; L. Bottou; Y. Bengio; P. Haffner, “Gradient-based learning applied to document recognition,” Proc. IEEE, vol. 86, no. 11, pp. 2278–2323, Nov. 1998. https://doi.org/10.1109/5.726791
• arrow_upward [46] N. J. Tustison; B. B. Avants; J. C. Gee, “Learning image-based spatial transformations via convolutional neural networks: A review,” Magn. Reson. Imaging, vol. 64, pp. 142–153, Dec. 2019. https://doi.org/10.1016/j.mri.2019.05.037
• arrow_upward [47] S. Vieira; W. H. Lopez Pinaya; A. Mechelli, Main concepts in machine learning.en Machine Learnin. Methods and Applications to Brain Disorders. Elsevier Inc., 2020. https://doi.org/10.1016/B978-0-12-815739-8.00002-X
• arrow_upward [48] Y. Lecun; Y. Bengio; G. Hinton, “Deep learning,” Nature, vol. 521, pp. 436–444, May 2015. https://doi.org/10.1038/nature14539