Proyección espacio-temporal del Covid-19 en Pereira

Recibido: 29 de Abril de 2020
Aceptado: 17 de Julio de 2020

Resumen

El brote actual de la enfermedad por coronavirus (COVID-19), que se informó por primera vez en Wuhan, China, el 31 de diciembre de 2019, ha dejado un saldo al 19 de abril de 2020 de más de 3500000 infectados y 160000 muertes en 185 países. En este trabajo utilizamos un modelo basado en el Método de Cadena Microscópica de Markov (MCMM, Markov Microscopic Chain Approach) para estimar la propagación del COVID-19 en la ciudad de Pereira (Risaralda-Colombia). Este modelo incorpora importantes aspectos de la población, relacionados con: ubicación espacial dentro de la ciudad discretizada por comunas, movilidad entre comunas, estratificación por grupos de edad y separación de individuos en siete compartimientos epidemiológicos. Este modelo se utiliza para predecir, en una línea de tiempo, la incidencia de epidemias en poblaciones geolocalizadas, lo que se traduce en una herramienta indicadora para tomar medidas de control. Así, el resultado de la metodología caracteriza la evolución en el tiempo y el espacio de la proporción de los individuos en cada uno de los compartimientos epidemiológicos y en cada grupo etario. Los datos que se refieren a COVID-19, desde la municipalidad de Pereira, hasta el 20 de abril de 2020, se utilizan para alimentar el modelo y obtener las proyecciones espacio-temporales. Los resultados presentados consideran múltiples escenarios de movilidad, de forma que el aplanamiento de las curvas de los diferentes compartimientos epidemiológicos pueda ser visualizados de acuerdo a diferentes estrategias de confinamiento. Por tratarse de un modelo espacio-temporal, los resultados del modelo pueden ser presentados fácilmente como mapas de calor sobre cada uno de los compartimientos epidemiológicos, a fin de facilitar los procesos de toma de decisiones.

Palabras clave: proyección espacio-temporal, propagación del COVID-19, Método de Cadena Microscópica de Markov, mapas de calor, Coronavirus.

Abstract

The current outbreak of coronavirus disease (COVID-19), which was first reported in Wuhan, China on December 31, 2019, has left a balance as of April 19, 2020 of more than 3500000 infected and 160000 deaths in 185 countries. In this work we use a model based on the Markov Microscopic Chain Approach (MMCA) to estimate the spread of COVID-19 in the city of Pereira (Risaralda-Colombia). This model incorporates important aspects of the population related to spatial location within the city which is discretized by communes, mobility between communes, stratification by age groups and separation of individuals into seven epidemiological compartments. This model is used to predict, in a timeline, the incidence of epidemics in geolocated populations, which translates into an indicator tool to take control measures. The data referring to COVID-19, from the municipality of Pereira, until April 20, 2020 are used to feed the model and obtain the spatio-temporal projections. The results presented consider multiple mobility scenarios, so that the flattening of the curves of the different epidemiological compartments can be visualized according to different confinement strategies. As it is a spatio-temporal model, the results of the model can easily be presented as heat over each of the epidemiological compartments, in order to facilitate decision-making processes.

Keywords: Spatio-temporal projection, spread of COVID-19, Markov Microscopic Chain Approach, heat maps, Coronavirus.

1. INTRODUCCIÓN

Es conocida la evolución del uso de los procesos de soldadura por arco Para estimar en el tiempo la propagación de enfermedades dentro de una sociedad se utilizan comúnmente técnicas del campo de la inteligencia artificial y métodos basados en la formulación de modelos matemáticos, todos ellos altamente susceptibles a la calidad y ajuste de los parámetros epidemiológicos más relevantes de la enfermedad analizada. Dentro de estos últimos métodos, los modelos basados en agentes han ganado gran relevancia al intentar modelar el comportamiento de la propagación de epidemias en redes complejas [1]. En este tipo de modelos un número finito de agentes microscópicos (compartimientos epidemiológicos) interactúan de acuerdo a suposiciones simples de comportamiento dentro de una red o grafo que proporciona un comportamiento observable macroscópico del sistema modelado. Estos agentes son enlazados dinámicamente, dentro de la red, utilizando la teoría de agregación de cadena de Markov [1].

Recientemente, en [2] se presenta un modelo basado en el Método de Cadena Microscópica de Markov (MCMM, Markov Microscopic Chain Approach) el cual es adaptado del modelo presentado en [3] y ajustado a las condiciones de la actual epidemia en España. El modelo utiliza las estimaciones de parámetros epidemiológicos y datos de censos demográficos y de movilidad y toma en cuenta varias importantes características específicas de la dinámica del COVID-19, tales como: i) el efecto de individuos infecciosos asintomáticos y ii) la fracción de individuos que requieren hospitalización en UCI.

Los eventos de importación y exportación del nuevo Coronavirus (SARS-CoV-2) son principalmente asociados a la movilidad de la población.

Adicionalmente, la evolución médica de la enfermedad COVID-19 ha presentado marcadas diferencias entre distintas franjas etarias de la población [2]. Tres aspectos fundamentales asociados a la transmisión del SARS-CoV-2 han sido establecidos claramente: i) la porción joven de la población puede transmitir el patógeno silenciosamente, ii) la movilidad de la porción adulta de la población tiene una alta probabilidad de diseminación del patógeno y iii) el COVID-19 produce en la porción de adultos mayores de la población fuertes síntomas y complicaciones que pueden incrementar dramáticamente la demanda de la red hospitalaria. Así, el modelo implementado considera siete compartimientos o estados epidemiológicos actuando sobre tres diferentes franjas etarias `G={a,b,c}`: joven `≤` 25 años (a), adulto entre 26 y 65 años (b) y adulto-mayor de 66 años en adelante (c).

Estos siete compartimientos epidemiológicos corresponden a individuos: susceptibles (S), expuestos (E), asintomáticos infectados (A), infectados sintomáticos (I), recuperados (R), hospitalizados (H) y muertos (D), por lo que el modelo resultante se denomina SEAIRHD. Muchos modelos clásicos han manejado diferentes tipos de compartimientos, tales como SIR [4], [5], [6], SEIR [6] and SEIJR [7], donde `J` corresponde a individuos diagnosticados.

Estos modelos mostraron ser inapropiados para describir la propagación de la enfermedad, principalmente porque no consideran la propagación durante el periodo de latencia. En [8], los autores presentan un modelo SEIR modificado basado en ecuaciones diferenciales ordinarias (ODE, por su acrónimo en inglés), que considera a los individuos aislados y el periodo de latencia. Este modelo resulta ser eficiente para estudiar la propagación de la enfermedad en una zona particular utilizando una menor cantidad de parámetros. Sin embargo, no permite analizar interacciones entre regiones ni entre franjas etarias.

Así, en este artículo se implementa y adapta el modelo propuesto en [2] al comportamiento actual de la epidemia en el municipio de Pereira (Risaralda-Colombia). El modelo permite caracterizar la evolución en el tiempo y el espacio de la proporción de los individuos en cada uno de los compartimientos epidemiológicos y en cada grupo etario. Los resultados son presentados por comunas y de forma dinámica en el tiempo.

2. MODELO DE PROPAGACIÓN DE LA EPIDEMIA BASADO EN COMPARTIMIENTOS EPIDEMIOLÓGICOS

Para modelar el comportamiento espacio-temporal de la epidemia, considerando los aspectos mencionados anteriormente, es necesario tener en cuenta que la población está distribuida en un conjunto de áreas (en nuestro caso comunas) caracterizadas por el número de individuos que, a su vez, son discriminados por franja etaria. En este modelo se supone que la probabilidad de transmisión entre individuos de la misma franja etaria es igual, mientras que para individuos de una franja etaria g con individuos de una franja `h`, la probabilidad de transmisión obedece a una matriz de contacto por edad `C`, cuyos elementos `C`^`gh` define la fracción de contactos que individuos de la franja `g` pueden tener con individuos de la franja `h`.

La movilidad entre comunas es representada como un grafo orientado, donde la comuna es un nodo de la red y el arco que conecta dos nodos representa la posibilidad de moverse entre los dos nodos que conecta. El peso ponderado del arco corresponde a un valor de movilidad normalizado suministrado por estudios previos [9], [10].

El modelo es compuesto de los siguientes siete compartimientos epidemiológicos (ver Fig. 1):

Fig. 1. Lógica del modelo SEAIRHD para un instante de tiempo t. Fuente: elaboración propia.

Susceptibles (S): corresponde al porcentaje de la población de una comuna en una franja etaria que es susceptible de contagio.

Expuestos (E): es la porción de individuos susceptibles de la comuna `i` y de la franja etaria `g` que son infectados (pero no infecciosos) con cierta probabilidad `π_i^g`. En los individuos expuestos la enfermedad se encuentra en su periodo de incubación o latencia, por lo cual no existen síntomas y no pueden infectar a otros.

Los individuos `E` son infectados por contacto con individuos asintomáticos con una infectividad `β_(A)` y sintomáticos con una infectividad `β_I`.

Asintomáticos (A): los individuos expuestos de la franja etaria `g` pasan a ser infectados asintomáticos a una razón de `η`^`g`. Los individuos `A` pueden infectar a otros,

Infectados (I): los individuos asintomáticos de la franja etaria `g` pasan a ser infectados (infectados con síntomas) a razón `α`^`g`. Los individuos `I` pueden ser hospitalizados o se pueden recuperar a una razón `μ`^`g`.

Hospitalizados en Unidad de Cuidados Intensivos - UCI (H): los individuos `I` pueden requerir hospitalización en UCI con cierta probabilidad `γ`^`g`.

Recuperados (R): Los individuos H se pueden recuperar con cierta probabilidad `1`-`y`^`g` y las UCIs se desocupan a una razón `χ`^`g`.

Muertos (D): Los individuos `H` tienen una probabilidad de muerte `ω`^`g` la cual se alcanza a una razón `ψ`^`g`.

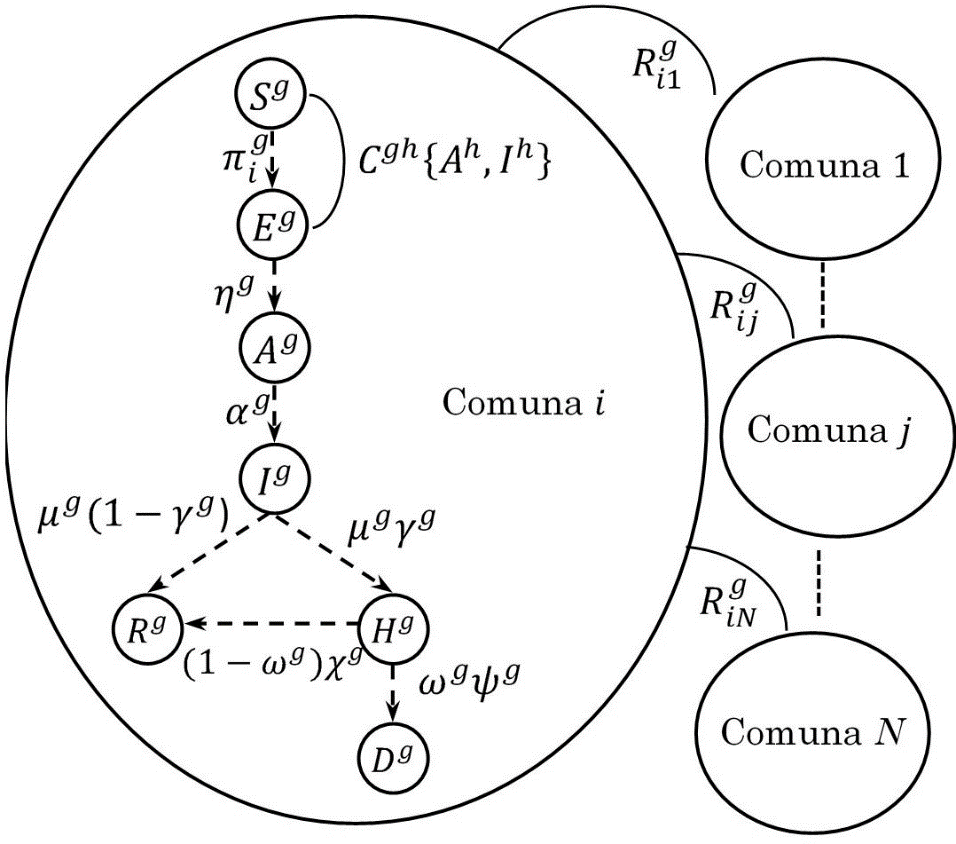
Estos siete compartimientos epidemiológicos conforman un modelo SEAIRHD cuyos estados se relacionan como se muestra en la Fig. 1.

Los individuos de la población de una comuna `i`, de la franja etaria `g` que son susceptibles a contagio `S`^`g`, pasan a ser individuos `E`^`g`, con cierta probabilidad `π_i^g` cuando entran en contacto con individuos Aho Ih de la franja etaria `h∈` `{a,b,c}`. Los contactos entre individuos de diferentes edades se modelan a través de la matriz de contacto C de dimensiones `N`_`G``×N`_`G`, donde `N`_`G` =3 porque se consideran 3 franjas etarias en este caso.

El contacto entre individuos de la franja g etaria con individuos de otras comunas del municipio se modela a través de una matriz de movilidad entre comunas `R``g`, de dimensiones `N×N`, donde el elemento `R_(ij)^g` denota la posibilidad de movilidad de los individuos de la franja entre las comunas `i` y `j`, como se indica en la Fig. 1. Por lo tanto, existe la probabilidad de que la enfermedad la contraigan individuos de la franja `g` dentro de la comuna de residencia (`CR_i^g`) por factores de contacto o la probabilidad de que se contraiga por factores de movilidad con comunas vecinas (`CV_i^g`).

La variable `π_i^(g)``(t)` se define como la probabilidad de que individuos `S^g` de la comuna `i` contraigan la enfermedad en un instante del tiempo `t`, por factores de movilidad o por factores de contacto. Por lo tanto, `π_i^(g)(t)` se calcula como la suma de las dos probabilidades anteriores, (1):

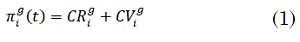
Para el cálculo de las probabilidades `CR_i^g` y `CV_i^g` es necesario calcular primero el parámetro `P_i^(g)(t)`, que denota la probabilidad de que los individuos del grupo `g` sean infectados por Coronavirus dentro de la comuna `i`. El cálculo de este parámetro se presenta en el Apéndice A.

Así, cada probabilidad se calcula de la siguiente manera en (1), (2) y (3)

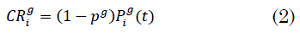
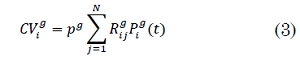
Donde, `p^g` es un factor de movilidad por edad que permite darle importancia relativa a cada una de las probabilidades.

El modelo permite caracterizar la evolución en el día `t` y la comuna `i` de la proporción de los individuos en cada uno de los compartimientos epidemiológicos `m∈{S,E,A,I,R,H,D}` y en cada grupo etario `g∈{a,b,c}`

Esta proporción de individuos se denota como `ρ_i^(m,g)(t)` y su cálculo se describe en la sección 4.

2.1 Algunos indicadores adicionales

Total de casos por comuna en un día `t` `CT_i(t)`: para una proyección en el tiempo del número total de casos, se deben sumar todos los individuos recuperados, hospitalizados y fallecidos en ese día, de acuerdo a (4):

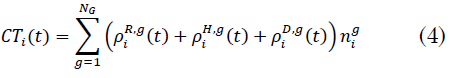
Donde, `n_i^g` es la población de la comuna `i` en la franja `g`.

Probabilidad de que un individuo viva en un hogar sin ningún individuo infectado `CH_i(t_ c)`: nótese que con el número total de individuos susceptibles y recuperados en un día `t_c` y con el número promedio de individuos por vivienda `σ`, es posible establecer la proporción de estos dos tipos de individuos por comuna y utilizarla para establecer el siguiente indicador (5), el cual se define como la probabilidad de que un individuo viva en un hogar sin ningún individuo infectado, dentro de una comuna `i`

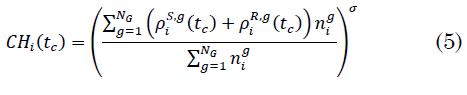
Este indicador permite cuantificar la eficiencia de una política de confinamiento ya que se esperaría que este decrezca en el tiempo a partir del día `t_c`.

3. RESTRICCIONES DE MOVILIDAD

En esta sección se presenta la incorporación de políticas de aislamiento en el modelo matemático, siguiendo la formulación presentada en [2]. Para ello se definen tres nuevos parámetros: i) la fracción de la población `k_0` que es aislada o confinada en casa, ii) el número promedio de individuos por vivienda `σ` en el municipio y iii) el día `t_c` en que se implementa la política de confinamiento.

Así, con `k_0=1` se modela el efecto de aislar las viviendas unas de las otras y con `k_0=0` se modela el efecto de una población “bien mezclada”, lo cual significa que la probabilidad de transmisión entre individuos de la misma franja etaria es igual.

Estos parámetros insertan un comportamiento dinámico en el tiempo en el parámetro `k_g` que representa el número promedio de contactos diarios por franja etaria, de acuerdo a (6)

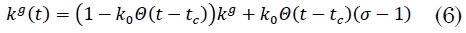
Donde, `Θ(x`) es la función escalón unitario.

Por lo tanto, los parámetros de movilidad también cambian dinámicamente como (7):

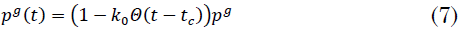
Las ecuaciones (6) y (7) influyen en el cálculo de la probabilidad `P_i^(g)(t)` que se desarrolla en el Apéndice A.

Adicionalmente permiten generar un nuevo compartimiento intermedio en el modelo que consiste en caracterizar la proporción de individuos aislados `ρ_i^(CH,g)`.

4. EVOLUCIÓN TEMPORAL DEL MODELO

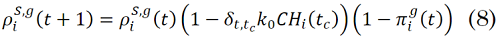
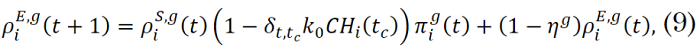
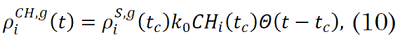
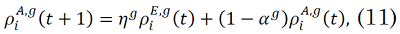
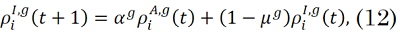
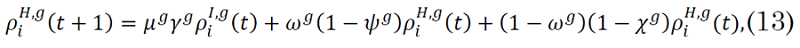
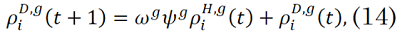
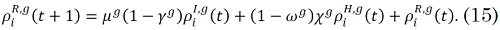
La evolución temporal de las proporciones de individuos en cada uno de los compartimientos epidemiológicos, tal como se presenta en [2] es dada por las ecuaciones (8), (9), (10), (11), (12), (13), (14) y (15).

Donde, `δ_(a,b)` es la función delta de Kronecker, la cual vale 1 si `a=b` y vale 0 si son diferentes. Las ecuaciones (8)-(15) suministran información discriminada por comuna, por día y por franja etaria.

5. RESULTADOS

El municipio de Pereira está ubicado en el departamento de Risaralda, Colombia.

Está conformado por 19 localidades, denominadas comunas, y posee una población de aproximadamente 470000 habitantes. El primer caso de COVID-19 en Pereira se reportó el 15 de marzo de 2020. El número de casos reportados en Pereira al 21 de abril de 2020 es de 88 y 4 personas fallecidas. En este trabajo, el modelo descrito anteriormente se utiliza para analizar la propagación de la enfermedad únicamente en Pereira, sin embargo, puede ser usado para un análisis nacional incorporando parámetros de movilidad intermunicipal y parámetros epidemiológicos ajustados. Tanto la matriz origen-destino de movilidad `R_(ij)^g` como las densidades poblacionales por comuna y por edad `n_i^g` han sido obtenidas de [4] y [5], respectivamente. La matriz de contacto entre franjas etarias `C^(gh)` y los parámetros epidemiológicos utilizados han sido tomada tal como se presentan en [2].

El periodo de incubación se ha determinado en [11] como `η^(-1)+α^(-1)= 5,2` días en promedio, por lo cual en el modelo implementado estos días se distribuyen entre los compartimiento `A` e `I`. En nuestro caso, el mejor ajuste se obtuvo considerando `η^(-1)=2,2` días en la fase A y `α^(-1)=3,0` días en la fase I. El periodo infeccioso de la enfermedad ha sido establecido como `μ^(-1)=3,2` días [12], [13].

En este caso se ha definido que para adultos y adultos-mayores `(μ^(-1))^(b,c)=3,2` días y en los individuos jóvenes `(μ^(-1))^a=1` día, lo cual significa que en los restantes 2,2 días los jóvenes se consideran infectados asintomáticos en la fase A

De acuerdo con [2], para todas las franjas etarias, la tasa de fatalidad de pacientes en UCI se asume como `ω=42 %`, el periodo desde la admisión en la UCI hasta la muerte se asume como `ψ^(-1)=7` días [14] y el periodo que un individuo permanece en UCI hasta recuperarse ha sido establecido como `χ=10` días [15]. Los parámetros utilizados se muestran en la Tabla 1 y son tomados de [2]

Tabla 1. Parámetros. Fuente: elaboración propia

Los datos recopilados hasta el 31 de marzo de 2020 son utilizados para inicializar el modelo. Hasta esta fecha el número de individuos por compartimiento epidemiológico era: 25 casos reportados, 17 recuperados, 98 expuestos, 1 fallecido y 2 hospitalizados.

5.1 Resultados para el actual estado de aislamiento

Para modelar la movilidad actual y un alto grado de confinamiento se utiliza `K_0= 0,8` y un factor de movilidad `p^g`= [0,1; 0,6; 0,3] desde el 31 de marzo de 2020.

Es decir, se asume que la movilidad en jóvenes es del 10 % debido a las actuales restricciones en horario y acceso a lugares públicos, 2 horas al día y sin salir del vehículo.

En adultos mayores se asume una movilidad del 30 % debido a que existen limitaciones en horario, pero con mayor acceso a lugares públicos. La movilidad en adultos es reducida al 50% a través de estrategias de confinamiento obligatorio por días. Dado que algunos individuos no obedecen esta instrucción, se asume una movilidad reducida del 60 % en adultos.

Los datos reales proyectados por el modelo, a partir del 1 de abril de 2020 son mostrados en la Fig. 2. Nótese que el día 16 de abril un evento atípico sucedió en una de las clínicas de la ciudad debido a un brote masivo que comprometió a 28 individuos. Este evento se incorpora al modelo de acuerdo con (16)

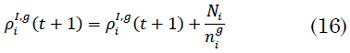
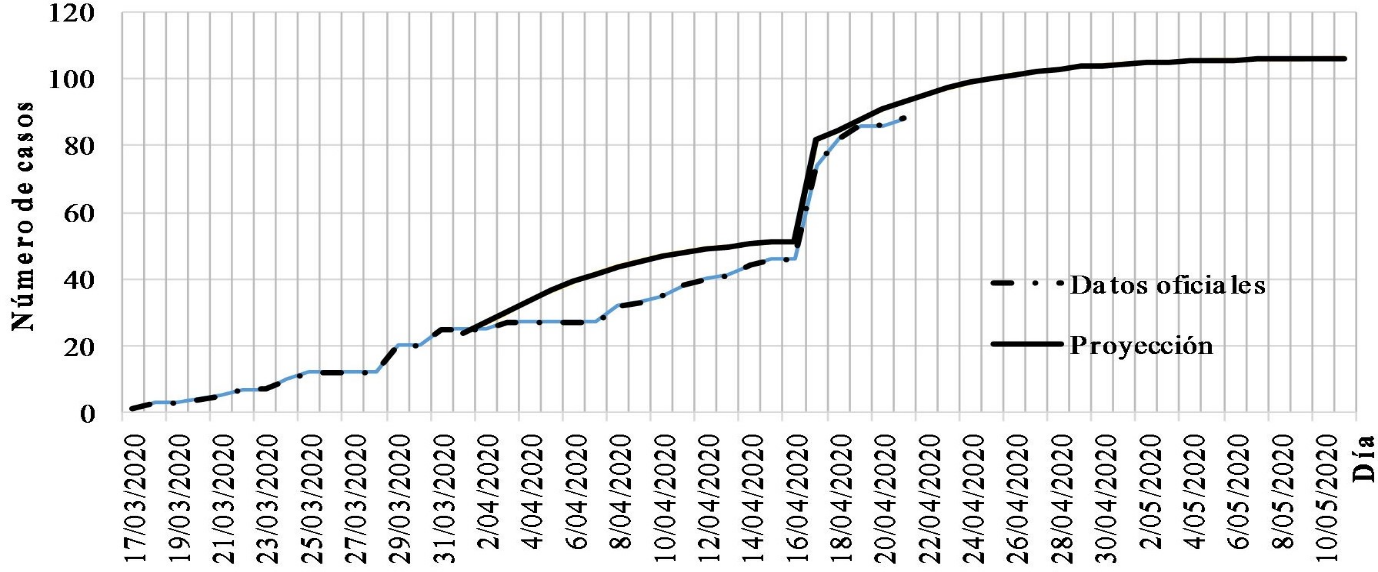
Fig. 2. Evolución de casos totales reportados en el municipio de Pereira. Fuente: elaboración propia.

El número de muertes diarias acumuladas reportadas y proyectadas es mostrado en la Fig. 3 considerando un alto nivel de confinamiento debido a la cuarentena obligatoria.

Fig. 3. Evolución de muertes totales. Fuente: elaboración propia.

La línea punteada no considera el efecto del brote presentado en una clínica de la ciudad el día 16 de abril, lo cual permite visualizar el impacto en número de muertes proyectadas de este evento.

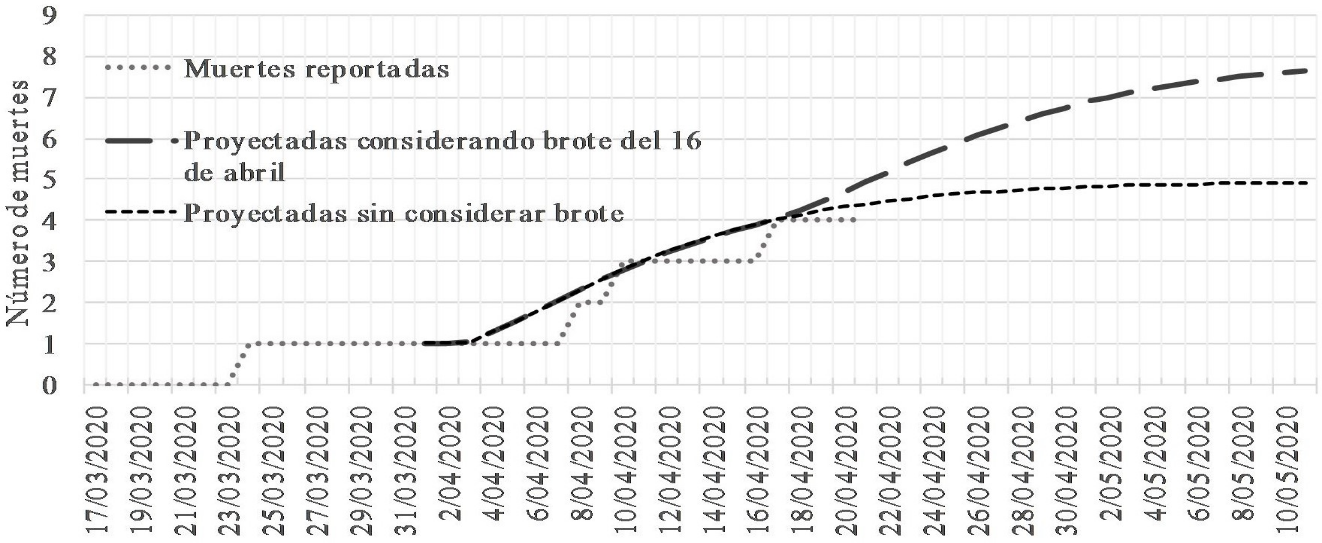
Para evaluar la congestión de la red hospitalaria en la ciudad, se presenta en la Fig. 4 el número acumulado de individuos hospitalizados reportados hasta el 21 de abril y proyectados hasta el 11 de mayo.

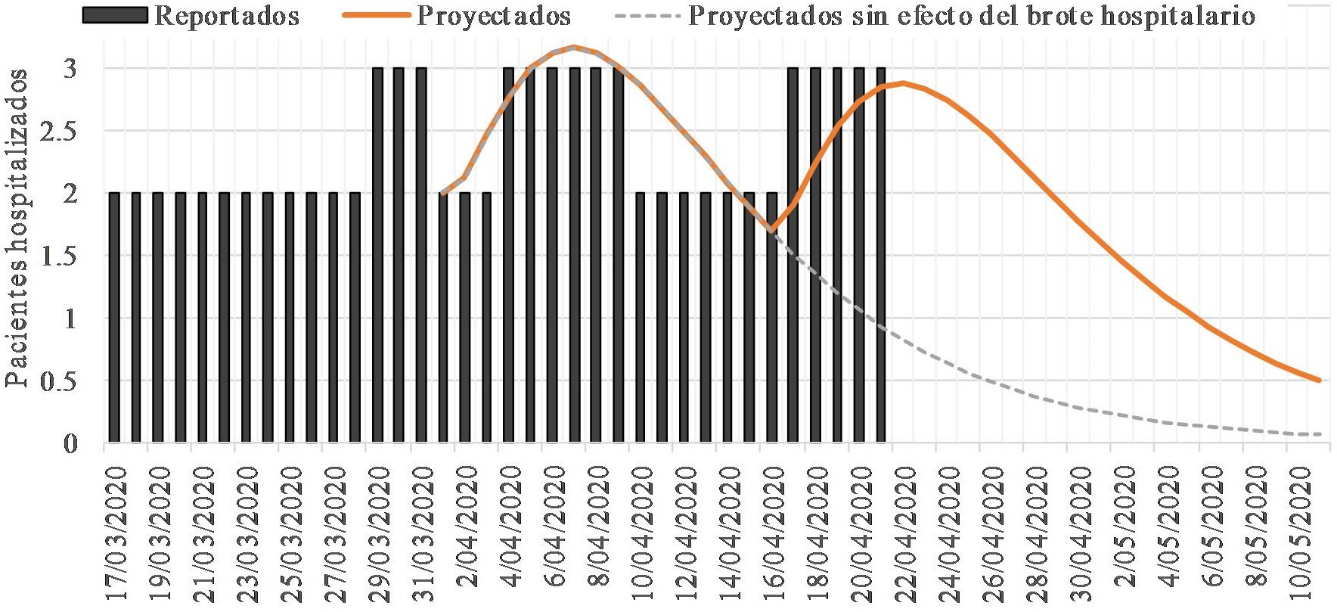
Fig. 4. Evolución diaria del número de hospitalizados en UCI. Fuente: elaboración propia.

La proyección arrojada por el modelo y los datos reales reportados, indican que un primer pico de hospitalizaciones se presentó entre el 4 y el 10 de abril, sin embargo, debido al evento de brote hospitalario, un segundo pico se proyecta entre los días 20 y 26 de abril. La gráfica en línea punteada muestra el comportamiento sin considerar el impacto del brote hospitalario.

La Fig. 5 muestra los casos oficiales reportados diariamente y el número diario de infectados proyectados por el modelo.

La relación de estas dos gráficas muestra que al inicio de la proyección el valor esperado de infectados era mucho mayor que el reportado. Posiblemente esto muestra la necesidad de realizar un mayor número de pruebas de laboratorio.

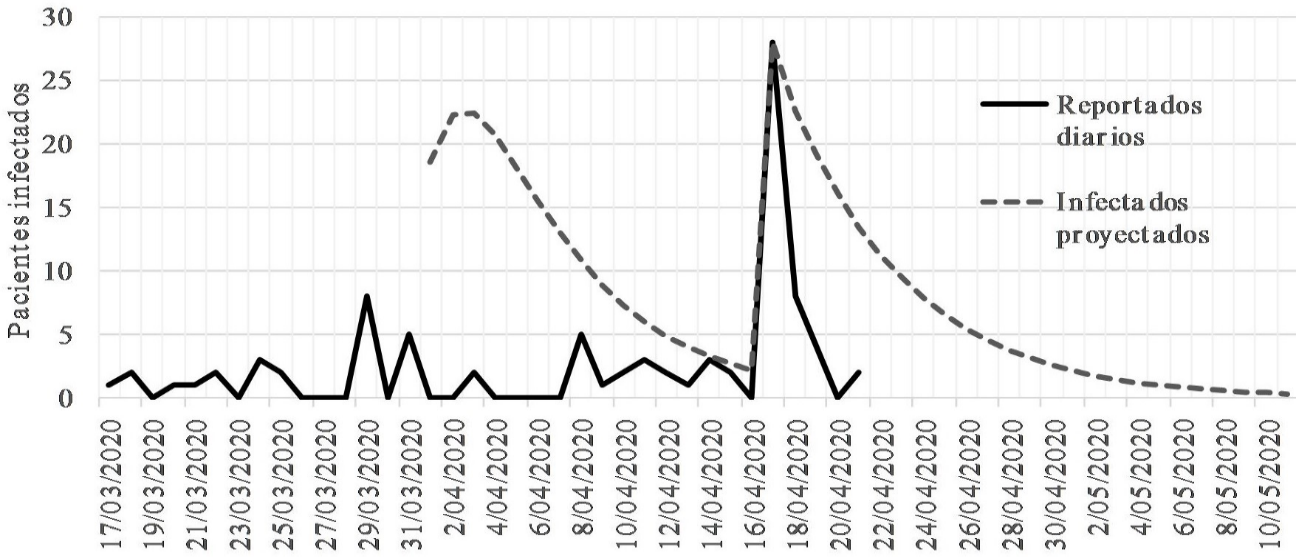
Fig. 5. Infectados diarios. Fuente: elaboración propia.

Sin embargo, al final del día 15 de abril se nota que las dos gráficas empiezan a coincidir, hasta que se presenta el evento de contagio masivo en una de las clínicas de la ciudad. A partir de allí, y hasta el día 21 de abril, el número proyectado de infectados sigue siendo considerablemente mayor que el número reportado, lo cual sugiere la necesidad de un mayor número de pruebas en la ciudad.

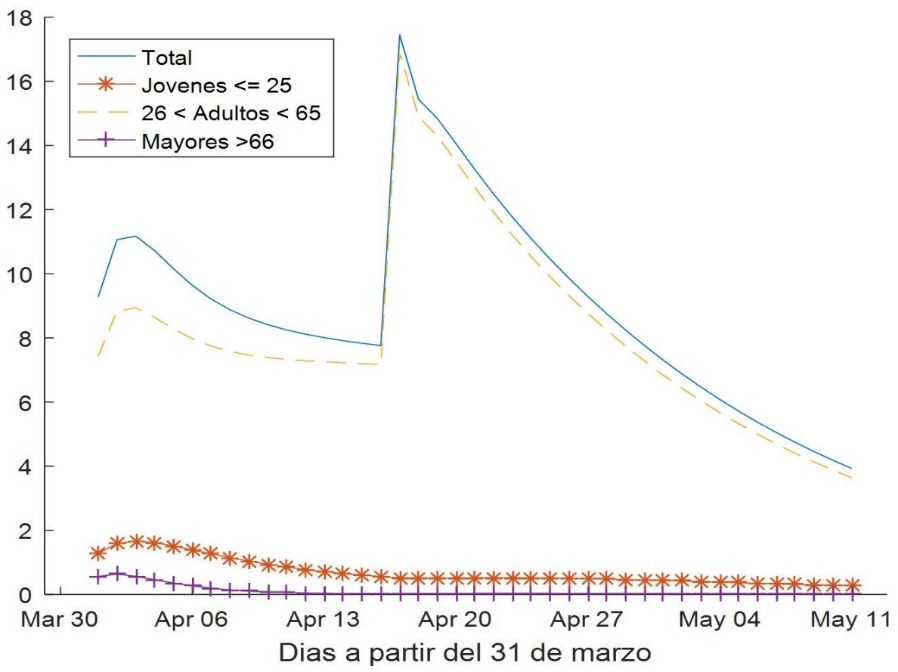
La Fig. 6 muestra la evolución del número diario de infectados asintomáticos, cuyo primer pico se estimó alrededor de 11 casos diarios en la primera semana de abril y después un segundo pico estimado alrededor de 18 casos diarios en la última semana de abril, debido al evento de contagio masivo. Nótese también que los resultados muestran el impacto del segundo pico principalmente en la población de adultos, debido a los porcentajes considerados de movilidad.

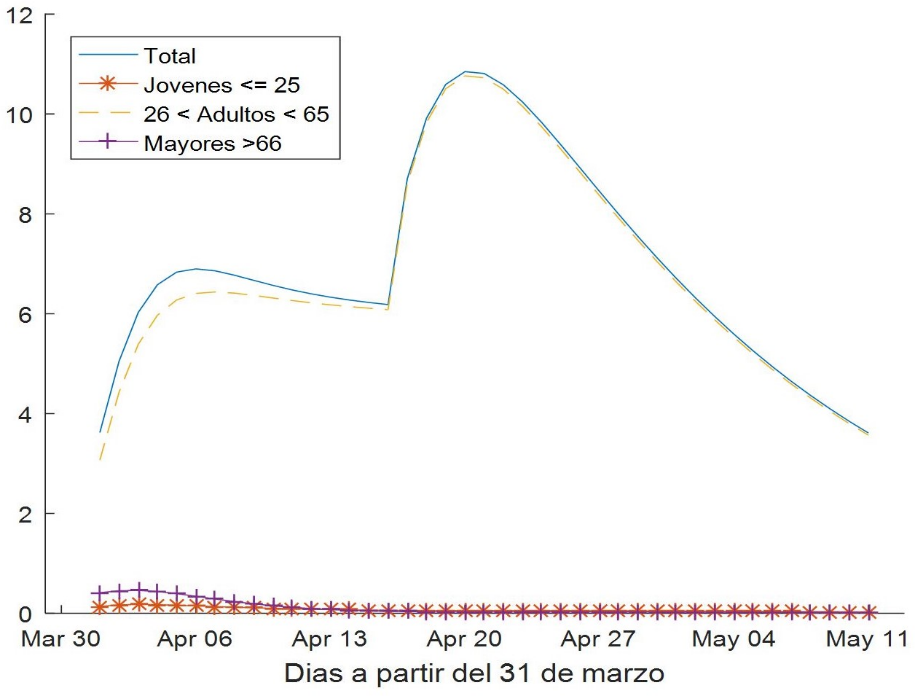
Fig. 6. Infectados asintomáticos. Fuente: elaboración propia.

La Fig. 7 muestra la evolución del número diario de infectados con síntomas.

Fig. 7. Infectados sintomáticos. Fuente: elaboración propia.

5.2 Resultados para diferentes escenarios de aislamiento desde el 19 de abril

En esta sección se presentan los resultados para diferentes escenarios de aislamiento considerados a partir del día 19 de abril y con movilidad únicamente en los individuos adultos, esto es: `p^g=[0,0; 1,0; 0,0]`. Una cuarentena total es definida por el factor `k_0=1`, indicando en el modelo que las viviendas son aisladas unas de las otras. Por otro lado, un factor `k_0=0` indica que la población está uniformemente mezclada y la probabilidad de contagio es la misma entre individuos de la misma comuna.

En la Fig. 8 se observa que, después del brote del 16 de abril, el número de hospitalizados en UCI incrementa aproximadamente 45% si no se realizan fuertes medidas de aislamiento. La evolución diaria de infectados (sintomáticos y asintomáticos), por escenarios, mostrada en la Fig. 9 permite estimar que bajo cuarentena total `(k_0=1)` es posible alcanzar el 11 de mayo con 0 infectados diarios. Por otro lado, sin confinamiento `(k_0=0)`, el 11 de mayo se tendría alrededor de 36 infectados diarios.

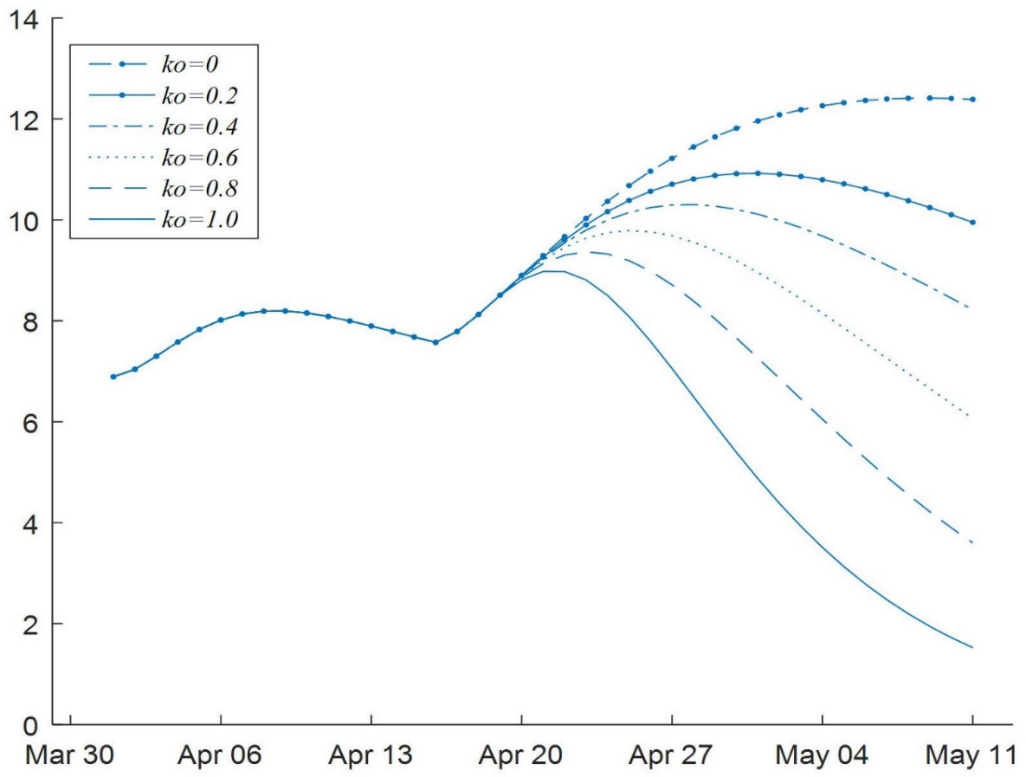
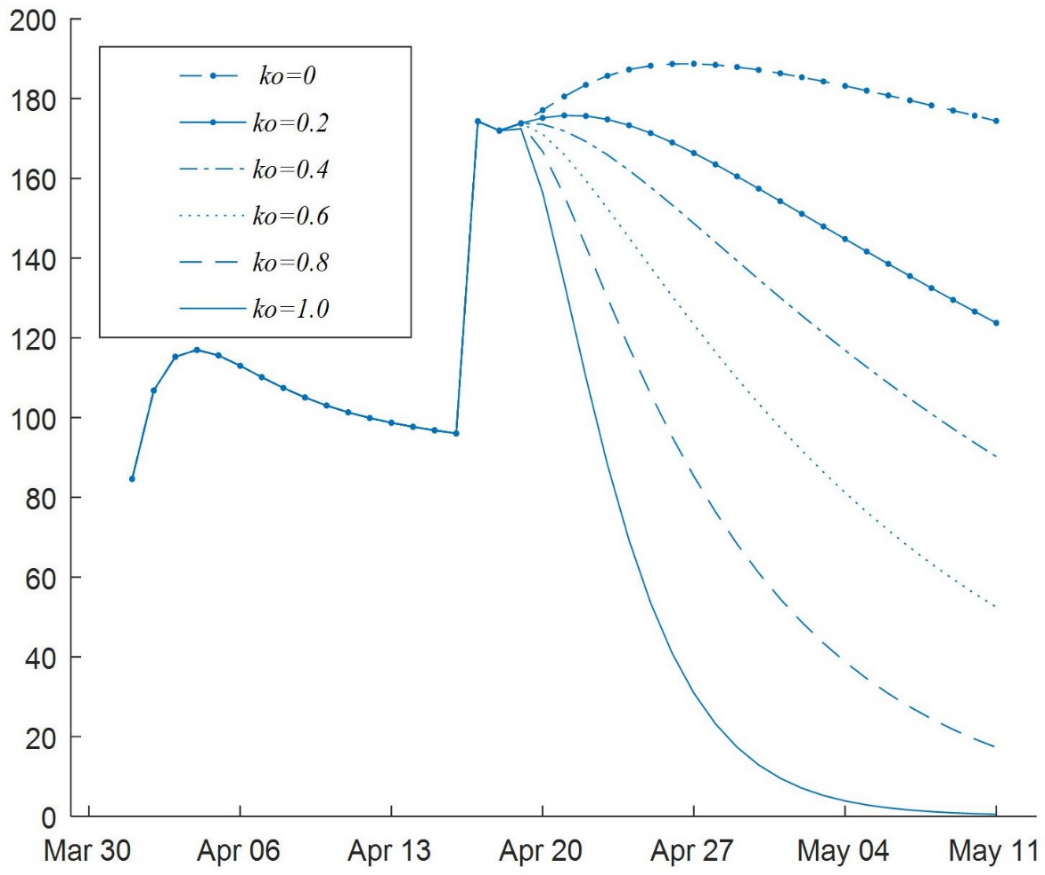
Fig. 8. Evolución de hospitalizados UCI. Fuente: elaboración propia.

Fig. 9. Estimación de infectados diarios. Fuente: elaboración propia.

Los puntos intermedios de aislamiento también muestran un alto número de infectados diarios.

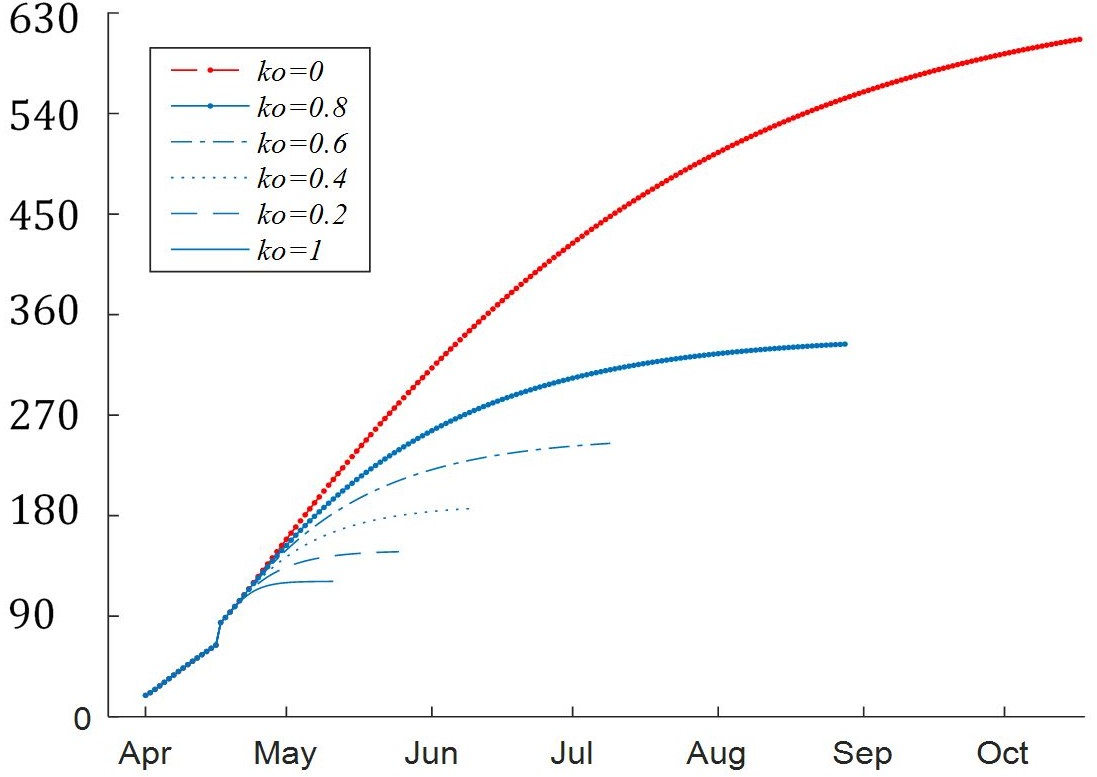
Las Fig. 10 y Fig. 11 muestran los diferentes escenarios de proyección para la evolución temporal del número total de casos y de fallecidos. La información espacio-temporal de cada compartimiento del modelo podría ser presentada en mapas de calor, como una herramienta de control y planeación.

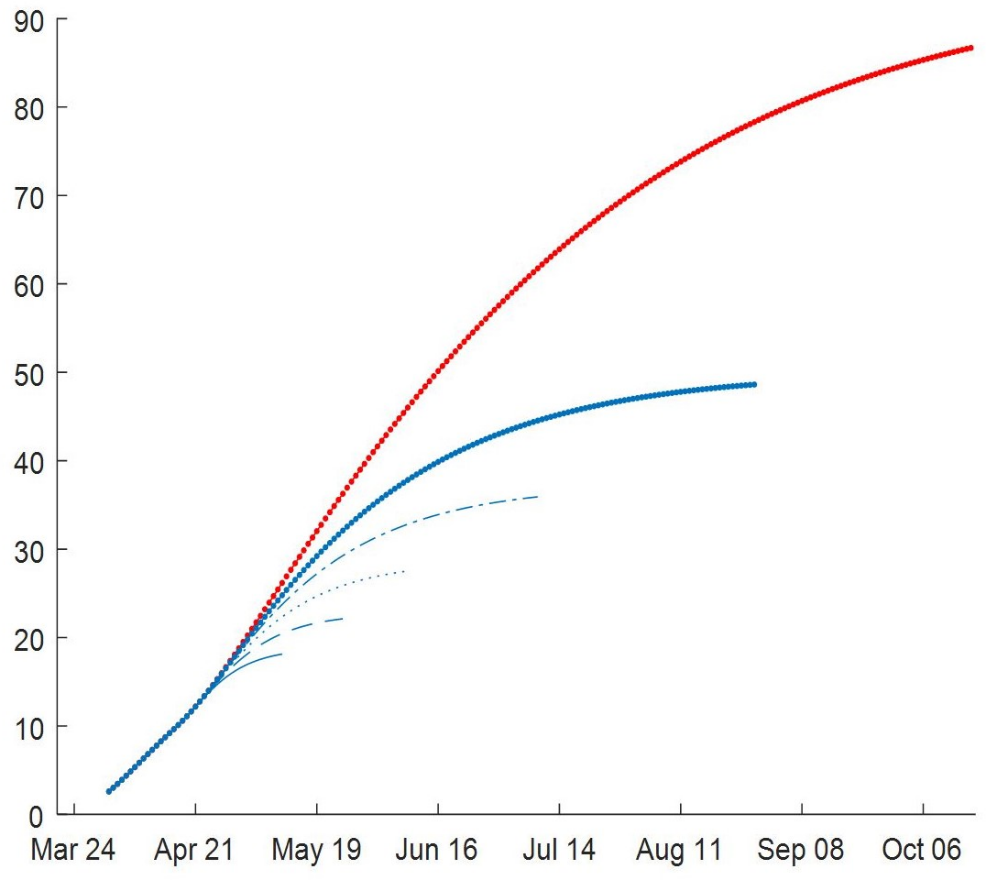
Fig. 10. Evolución del número de casos. Fuente: elaboración propia.

Fig. 11. Evolución de muertes. Fuente: elaboración propia.

A manera de ejemplo, la Fig. 12 muestra el caso de individuos infectados asintomáticos (compartimiento A) el día 4 de abril de 2020.

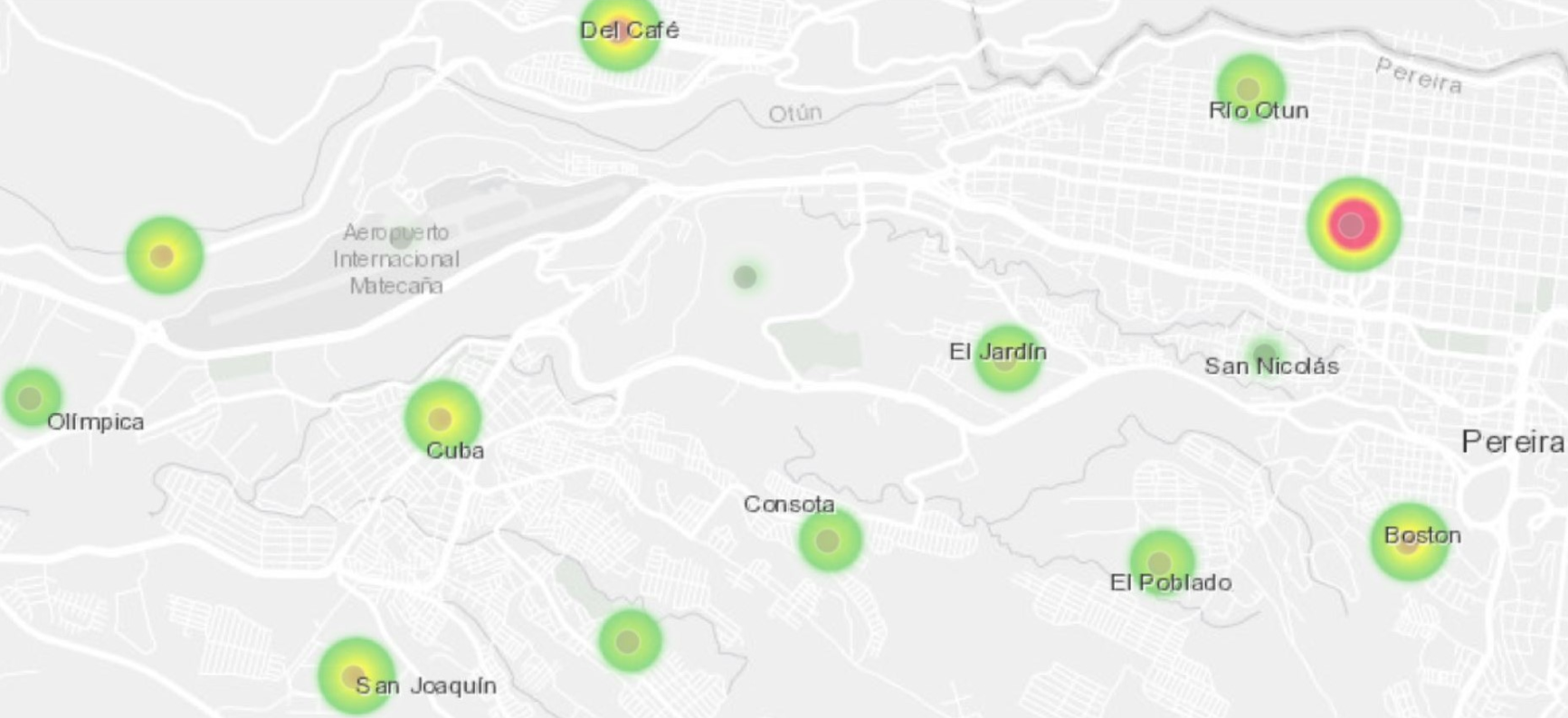
Fig. 12. Proyección espacial para infectados asintomáticos. Fuente: elaboración propia.

La Fig. 13, muestra por comuna y por franja etaria la proyección temporal del número estimado de pacientes en UCI.

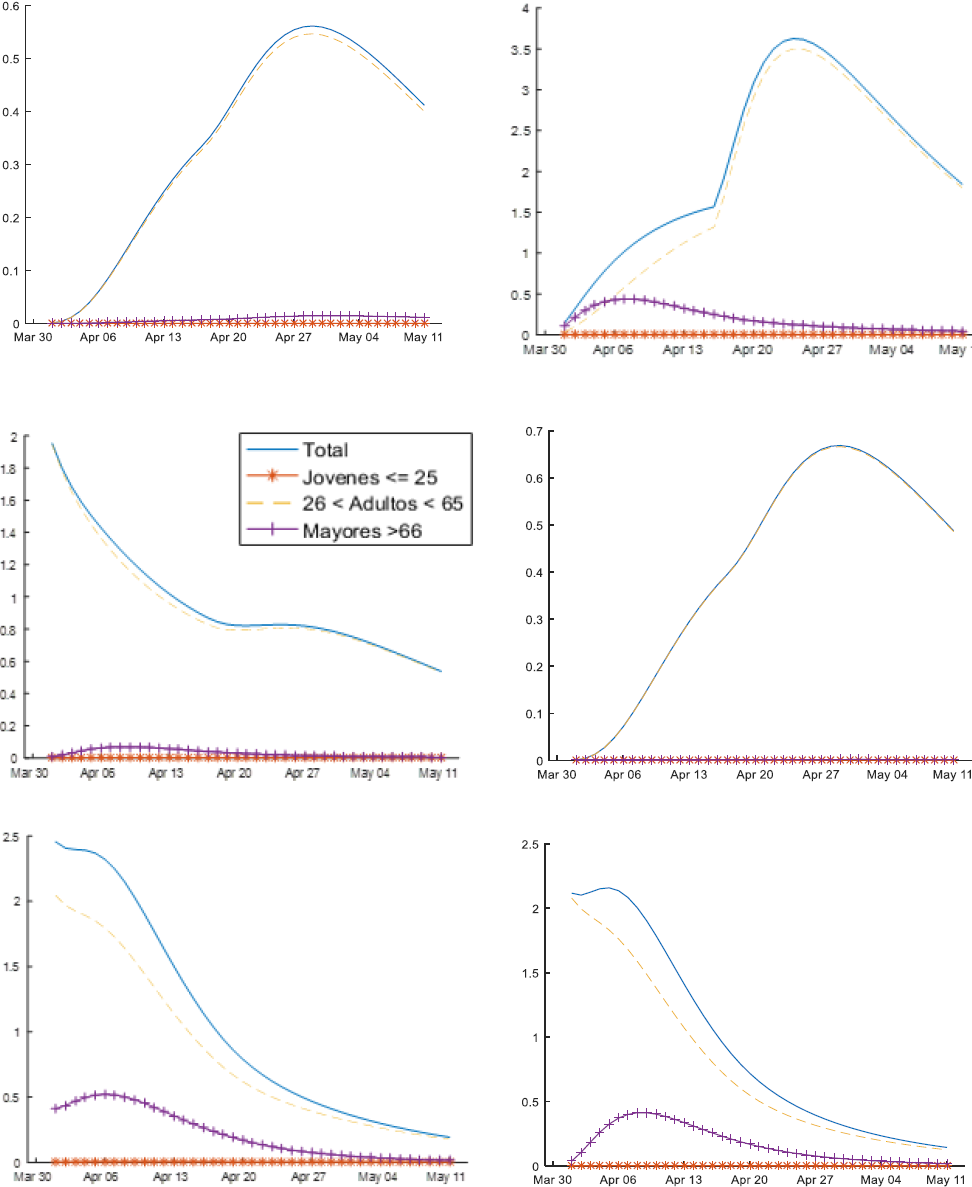
Fig. 13. Proyección espacio-temporal del número estimado de pacientes en UCI. Fuente: elaboración propia.

Sólo se muestran las comunas en donde el pico alcanzó un valor igual o superior a 0,5. Nótese que en esta figura es posible ver las comunas más sensibles al brote del 16 abril. La clínica con el brote está ubicada en la comuna Centro, la cual sufre un pico el día 25 de abril de 3 pacientes en UCI. Por las características particulares de movilidad definidas para Pereira y por la distribución del número de individuos por franja etaria dentro de cada comuna, las comunas más sensibles al brote son Olímpica y Del Café, con un número estimado de pacientes en UCI cercano a 2.

Estas comunas están fuertemente interconectadas con la comuna Centro.

6. DISCUSIÓN

En este trabajo se ha implementado un modelo espacio-temporal SEIR modificado, que considera tres franjas etarias, diferentes niveles de aislamiento de la población y siete compartimientos epidemiológicos, entre los cuales se encuentran los individuos asintomáticos, que constituyen una importante población de análisis en el contexto del comportamiento de la enfermedad COVID-19.

Los resultados obtenidos para los diferentes escenarios de aislamiento muestran que es necesario un aislamiento fuerte a partir del 19 de abril para contrarrestar los efectos del brote del 16 de abril y tener una reducción significativa en la incidencia de casos (alrededor de 150 casos) y una estabilización temprana en el número de muertes (alrededor de 20) al final de la primera semana de mayo. Para otros factores de aislamiento el número de casos podría superar los 600 y las muertes estabilizasen alrededor de las 100, en el mes de septiembre.

El modelo presentado es altamente sensible a los parámetros epidemiológicos utilizados. No obstante, el ajuste de estos parámetros puede basarse en: conocimiento de casos similares, históricos, criterio experto o metodologías basadas en aprendizaje de máquina, entre otras. Por otro lado, el modelo considera parámetros de contacto entre franjas etarias y movilidad entre comunas, así como también información demográfica de cada comuna discriminada por franjas de edad.

El ajuste y consecución de este tipo de información se consolida como una de las principales dificultades en la aplicación y utilización de este tipo de modelos epidemiológicos.

La aplicación del modelo en un municipio dividido por comunas y con poca población implica que la capacidad del sistema de salud se agrupa y se asigna al municipio debido a que muchas comunas carecen de capacidad hospitalaria propia.

La aplicación del modelo a una escala mayor, en donde por ejemplo las regiones son municipios, las capacidades del sistema de salud son individuales y el tiempo requerido por paciente en UCI podría ser diferente para cada municipio.

El código fuente del modelo implementado en Matlab® está disponible en: https://www.researchgate.net/publication/342192269_Implementacion_en_Matlab_del_Modelo_espacio-temporal_CIVID-19.

Este desarrollo puede ser usado para análisis dinámicos posteriores de sensibilidad de los resultados frente a variaciones de otros parámetros, tales como la matriz de contacto entre franjas etarias, diferentes matrices de movilidad y diferentes tasas de infección, entre otras.

Este tipo de análisis dinámico puede, eventualmente, proporcionar indicadores de alerta en función de dos características, la comuna y la franja etaria. Esto permitiría a los tomadores de decisiones realizar, por ejemplo, estrategias de confinamiento sectorizadas en función de estas dos características.

6.1. APENDICE: CÁLCULO DE `P`_`i`^`g``(t)`

El parámetro `P_i^(g)(t)` denota la probabilidad de que los individuos del grupo `g` sean infectados por Coronavirus dentro de la comuna `i`, se define en [2] como (17):

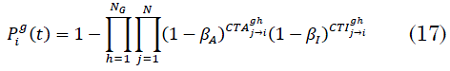
Donde, la doble multiplicatoria define la probabilidad de que un individuo que pertenece a la franja `g` no se infecte mientras está en la comuna `i`.

El exponente `CTA _(j→i) ^(gh)` reprepresenta el número de contactos realizados por un individuo que vive en la comuna `j` y pertenece a la franja etaria `g` con individuos del compartimiento `A` que viven en la comuna y pertenecen a la franja etaria `h`. El exponente `CTI_(j→i) ^(gh)` se define similarmente pero considerando los contactos con individuos del compartimiento `I`. El cálculo de estos exponentes es en (18), (19):

Donde, `NTC` es el número total de contactos (infecciosos o no) y `PC_A` y `PC_I` son la probabilidad de que estos contactos sean infecciosos del compartimiento `A` e `I`, respectivamente, los cuales se calculan así (20), (21), (22):

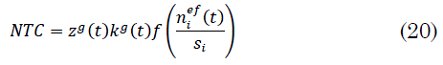
Donde, `z^g` es un factor de normalización dado por (23):

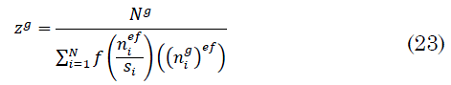
Donde, la población efectiva de la comuna es dada por (24):

La cual se distribuye en franjas etarias de acuerdo a (25):

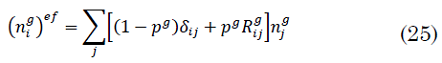
La funcion `f` amortigua la influencia de la densidad de la población de acuerdo con (26):

Finalmente, el número esperado de individuos de la franja etaria h en el compartimiento `m∈ {A,I}` que se ha movido de la región `j` a la región `i`, es dado por(27):

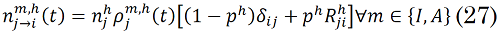
7. CONFLICTO DE INTERÉS DE LOS AUTORES

No se declaran conflictos de intereses por ninguno de los autores.

8. REFERENCIAS

[1] S. Banisch, “Markov Chain Aggregation for Agent-Based Models” en Understanding Complex Systems, Springer, Switzerland, 2016. https://doi.org/10.1007/978-3-319-24877-6
[2] A. Arenas et al., “A mathematical model for the spatiotemporal epidemic spreading of COVID19,” medRxiv, pp. 1-13, Mar. 2020. https://doi.org/10.1101/2020.03.21.20040022
[3] S. Gómez; A. Arenas; J. Borge-Holthoefer; S. Meloni; Y. Moreno, “Discrete-time Markov chain approach to contact-based disease spreading in complex networks”. EPL (Europhysics Letters), vol. 89, no. 3, pp. 1-6, Feb. 2010. https://doi.org/10.1209/0295-5075/89/38009
[4] Y. Chen; J. Cheng; Y. Jian; K. Liu, “A time delay dynamical model for outbreak of 2019-nCoV and the parameter identification”. Journal of Inverse and Ill-posed Problems, vol. 28, no. 2, pp. 243-250. Mar. 2020. https://doi.org/10.1515/jiip-2020-0010
[5] B. Cantó; C. Coll; E. Sánchez, “Estimation of parameters in a structured SIR model”. Advances in Difference Equations, vol. 1, no. 33, pp. 33, Jan. 2017. https://doi.org/10.1186/s13662-017-1078-5
[6] S. Ma. Stefan; Y. Xia, “Mathematical Understanding of Infectious Disease Dynamics” en Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore: vol. 16. 2008. https://doi.org/10.1142/7020
[7] C. Liu; G. Ding; J. Gong; L. Wang; K. Cheng; D. Zhang, “Studies on mathematical models for SARS outbreak prediction and warning” Chinese Sci Bull., vol. 49, no. 21, pp. 2245-2251, 2014. https://doi.org/10.1360/csb2004-49-21-2245
[8] R. E. González, “Different scenarios in the Dynamics of SARS-Cov-2 Infection: an adapted ODE model”. Populations and Evolution, 2020. https://arxiv.org/abs/2004.01295
[9] Observatorio de movilidad vial en Pereira, Universidad Tecnológica de Pereira (UTP), Pereira, Risaralda, 2019.: https://www.researchgate.net/profile/Mauricio_Granada-Echeverri/publication/342183390_PROYECCION_ESPACIO-TEMPORAL_DEL_COVID-19_EN_PEREIRA/data/5ee7caa692851ce9e7e47622/DatosCovidPereira.zip
[10] Departamento Administrativo Nacional de estadísticas, “Resultados Censo Nacional de población y Vivienda 2018”, 2019. https://www.dane.gov.co/index.php/estadisticas-por-tema/demografia-y-poblacion/censo-nacional-de-poblacion-y-vivenda-2018
[11] Q. Li, et al., “Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia”, The New Engl J Med., no. 382, pp. 1199-1207, Mar. 2020. https://doi.org/10.1056/NEJMoa2001316
[12] J. M. Read; J. R. Bridgen; D. A. Cummings; A. Ho; C. P. Jewell, “Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions,” MedRxiv, Jan. 2020. https://doi.org/10.1101/2020.01.23.20018549
[13] L. Danon; E. Brooks-Pollock; M. Bailey; M. J. Keeling. “A spatial model of CoVID-19 transmission in England and Wales: early spread and peak timing,” MedRxiv, pp. 1- 10, Feb. 2020. https://doi.org/10.1101/2020.02.12.20022566
[14] N. Wilson; A. Kvalsvig; L. T. Barnard; M. G. Baker. “Case-fatality risk estimates for covid-19 calculated by using a lag time for fatality,” Emerging Infectious Diseases, vol. 26, no. 6, Jun. 2020. https://dx.doi.org/10.3201/eid2606.200320
[15] H. Nishiura; N. M. Linton; A. R. Akhmetzhanov, “Serial interval of novel coronavirus (covid-19) infections,” International Journal of Infectious Diseases, vol. 93, pp. 284-286, Apr. 2020. https://doi.org/10.1016/j.ijid.2020.02.060

9. CONTRIBUCIÓN DE LOS AUTORES

¹ Conceptualización del modelo matemático e implementación.

²Conceptualización del modelo matemático e implementación.

³ Validación y análisis de resultados.